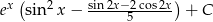Zadanie nr 8016799
Oblicz całkę 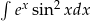 .
.
Rozwiązanie
Pozbędziemy się kwadratu przy sinusie korzystając z tożsamości
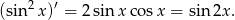
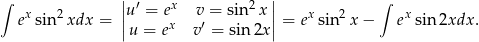
Ostatnią całkę oznaczamy przez 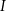 i liczymy
i liczymy
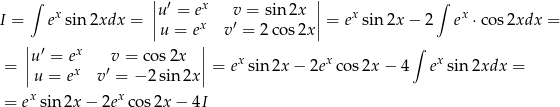
Zatem
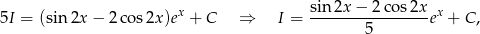
oraz
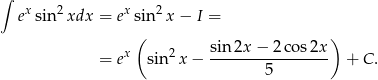
Odpowiedź: 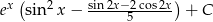
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 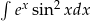 .
.
Pozbędziemy się kwadratu przy sinusie korzystając z tożsamości
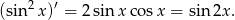
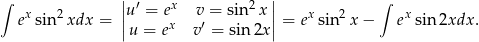
Ostatnią całkę oznaczamy przez 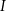 i liczymy
i liczymy
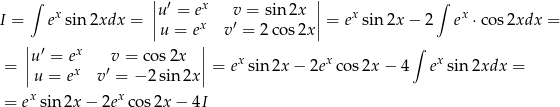
Zatem
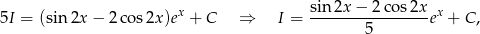
oraz
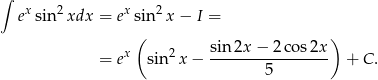
Odpowiedź: