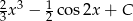/Studia/Analiza/Całki nieoznaczone/Różne

Zadanie nr 9519607

Oblicz całkę 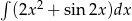∫ 2 (2x + sin 2x)dx .

Wersja PDF

Rozwiązanie

Myślimy: jaka musi być funkcja, żeby jej pochodną było 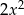2 2x ? Na pewno musi być 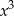x3 , ale licząc pochodną „na dół spadnie 3”, więc musimy dopisać z przodu 23 , żeby otrzymać współczynnik 2.

Podobnie z 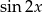sin 2x : funkcją pierwotną będzie 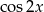co s2x , ale licząc pochodną z 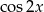cos2x otrzymamy współczynnik 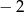− 2 (2 jest z pochodnej wnętrza). Zatem musimy z przodu dopisać 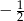1 − 2 (żeby otrzymać współczynnik 1). Zatem

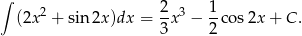
∫ (2x 2 + sin 2x)dx = 2-x3 − 1-cos2x + C . 3 2

 
Odpowiedź: 23x3 − 12 co s2x + C

Wersja PDF