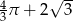/Szkoła podstawowa/Geometria/Okrąg i koło

Zadanie nr 4751832

Dodaj do ulubionych
Dodaj do rozwiązanych

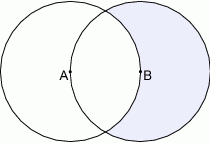
Na rysunku przedstawiono dwa koła o promieniu 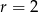r = 2 takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury.

PIC

Rozwiązanie

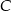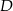Zauważmy, że gdy połączymy środki danych kół oraz ich punkty wspólne C i D , to otrzymamy dwa trójkąty równoboczne o boku r = 2 .

PIC

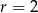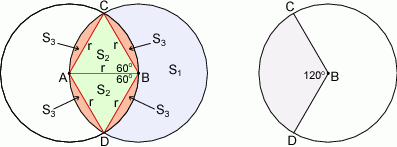
Pole każdego z tych trójkątów jest równe

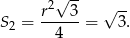
2√ -- S = r---3-= √ 3. 2 4

Łatwo też obliczyć pole wycinka kołowego przedstawionego w prawej części rysunku – jego pole stanowi 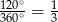120∘∘ = 1 360 3 pola całego koła, czyli jest równe

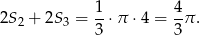
1 4 2S 2 + 2S 3 = 3-⋅π ⋅ 4 = 3π .

Mamy zatem

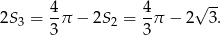
4- 4- √ -- 2S3 = 3π − 2S2 = 3 π − 2 3.

Możemy teraz obliczyć pole interesującej nas figury

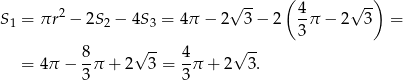
( ) 2 √ -- 4- √ -- S 1 = πr − 2S 2 − 4S 3 = 4π − 2 3− 2 3 π − 2 3 = 8 √ -- 4 √ -- = 4π − -π + 2 3 = --π + 2 3. 3 3

 
Odpowiedź: √ -- 43π + 2 3

Wersja PDF