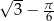Zadanie nr 8114313
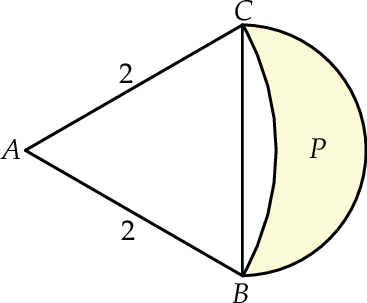
Trójkąt 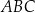 jest trójkątem równobocznym o boku długości 2. Obszar
jest trójkątem równobocznym o boku długości 2. Obszar 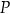 jest zawarty między półokręgiem o średnicy
jest zawarty między półokręgiem o średnicy 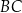 i łukiem okręgu o środku
i łukiem okręgu o środku 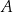 przechodzącym przez punkty
przechodzącym przez punkty 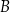 i
i 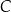 . Oblicz pole obszaru
. Oblicz pole obszaru 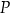 .
.
Rozwiązanie
Pole półkola o średnicy 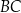 jest równe
jest równe
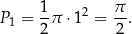
Od tego pola musimy odjąć pole 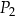 odcinka kołowego zawartego między odcinkiem
odcinka kołowego zawartego między odcinkiem 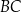 i łukiem
i łukiem 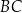 . Pole tego odcinka obliczamy jako różnicę pola wycinka kołowego o kącie
. Pole tego odcinka obliczamy jako różnicę pola wycinka kołowego o kącie 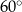 i pola trójkąta równobocznego
i pola trójkąta równobocznego 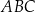 .
.
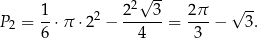
Pole obszaru  jest więc równe
jest więc równe
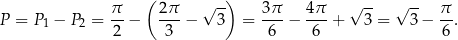
Odpowiedź: