Zadanie nr 9916522
Oblicz miarę kąta wpisanego opartego na średnicy okręgu.
Rozwiązanie
Powiedzmy, że kąt 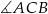 jest oparty na średnicy
jest oparty na średnicy 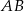 okręgu.
okręgu.
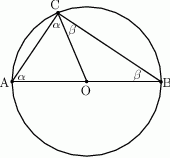
Poprowadźmy promień 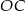 i oznaczmy
i oznaczmy 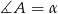 i
i 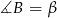 . Trójkąty
. Trójkąty 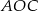 i
i 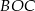 są równoramienne, więc
są równoramienne, więc 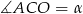 i
i 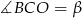 . Stąd
. Stąd
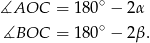
Suma tych dwóch kątów jest równa 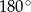 , skąd
, skąd
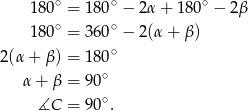
Odpowiedź: