/Studia/Analiza/Całki nieoznaczone/Wymierne/Mianownik stopnia 4

Zadanie nr 9406889

Oblicz całkę 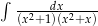∫ ----dx------ (x2+ 1)(x2+x) .

Wersja PDF

Rozwiązanie

Ponieważ

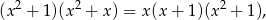
2 2 2 (x + 1)(x + x) = x(x + 1 )(x + 1),

szukamy rozkładu funkcji podcałkowej na ułamki proste w postaci:

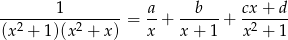
1 a b cx + d ----------------- = --+ ------+ ------- (x 2 + 1)(x 2 + x ) x x + 1 x 2 + 1

Mnożąc obie strony przez 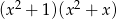(x2 + 1)(x2 + x) otrzymujemy

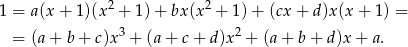
2 2 1 = a(x + 1 )(x + 1)+ bx (x + 1)+ (cx+ d)x(x + 1) = = (a + b + c)x3 + (a + c+ d)x2 + (a+ b+ d)x + a.

Porównujemy teraz współczynniki przy kolejnych potęgach x .

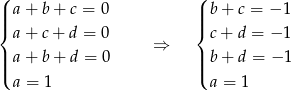
( ( ||| a+ b+ c = 0 ||| b+ c = − 1 { a+ c+ d = 0 { c+ d = − 1 | a+ b+ d = 0 ⇒ | b+ d = − 1 ||( ||( a = 1 a = 1

Jeżeli od pierwszego równania odejmiemy trzecie i dodamy drugie to otrzymamy 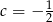c = − 1 2 . Stąd 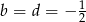b = d = − 1 2 oraz

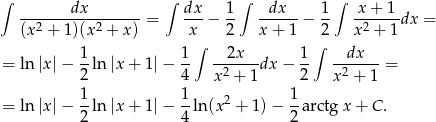
∫ ∫ ∫ ∫ -------dx--------= dx-− 1- -dx---− 1- x-+-1-dx = (x2 + 1)(x2 + x) x 2 x+ 1 2 x2 + 1 1 1 ∫ 2x 1 ∫ dx = ln|x| − --ln|x + 1|− -- --2----dx − -- -2-----= 2 4 x + 1 2 x + 1 = ln|x| − 1-ln|x + 1|− 1-ln (x2 + 1)− 1-arctg x + C . 2 4 2

 
Odpowiedź: 1 1 2 1 ln |x |− 2 ln|x + 1|− 4 ln(x + 1 )− 2 arctgx + C

Wersja PDF