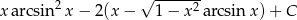Zadanie nr 8978183
Oblicz całkę 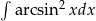 .
.
Rozwiązanie
Całkujemy przez części.
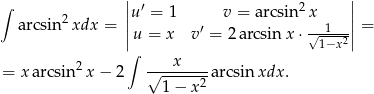
Zauważmy, że 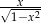 jest pochodną funkcji
jest pochodną funkcji 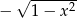 (łatwo to sprawdzić, różniczkując ostatnią funkcję), możemy więc raz jeszcze całkować przez części.
(łatwo to sprawdzić, różniczkując ostatnią funkcję), możemy więc raz jeszcze całkować przez części.
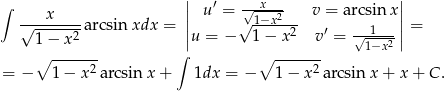
Mamy więc
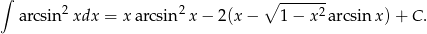
Odpowiedź: 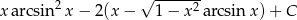
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 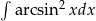 .
.
Całkujemy przez części.
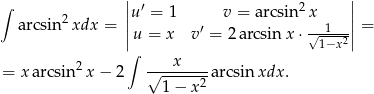
Zauważmy, że 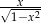 jest pochodną funkcji
jest pochodną funkcji 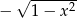 (łatwo to sprawdzić, różniczkując ostatnią funkcję), możemy więc raz jeszcze całkować przez części.
(łatwo to sprawdzić, różniczkując ostatnią funkcję), możemy więc raz jeszcze całkować przez części.
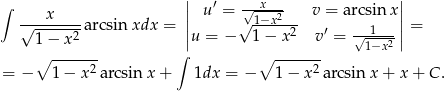
Mamy więc
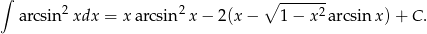
Odpowiedź: