/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Prostokątny/Pole

Zadanie nr 9292305

Dodaj do ulubionych
Dodaj do rozwiązanych

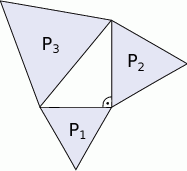
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne, których pola są odpowiednio równe 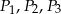P1,P 2,P 3 . Wówczas

PIC

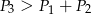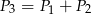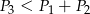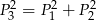
A) P3 > P1 + P2 B) P 3 = P1 + P2 C) P3 < P 1 + P 2 D) P23 = P21 + P22

Rozwiązanie

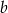Oznaczmy przez a i b długości przyprostokątnych, a przez c długość przeciwprostokątnej. Wówczas z twierdzenia Pitagorasa mamy

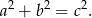
a2 + b2 = c2.

Liczymy

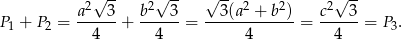
2√ -- 2√ -- √ -- 2 2 2√ -- P + P = a---3-+ b---3-= ---3(a-+-b--)= c---3-= P . 1 2 4 4 4 4 3

 
Odpowiedź: B

Wersja PDF