Zadanie nr 7162601
Funkcja kwadratowa 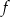 określona jest wzorem
określona jest wzorem 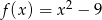 . Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą
. Aby wykres tej funkcji miał dokładnie jeden punkt wspólny z prostą 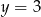 , należy go przesunąć o
, należy go przesunąć o
A) 12 jednostek w prawo wzdłuż osi 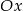
B) 12 jednostek do góry wzdłuż osi 
C) 12 jednostek do dołu wzdłuż osi 
D) 3 jednostki w lewo wzdłuż osi 
Rozwiązanie
Zaczynamy od rysunku
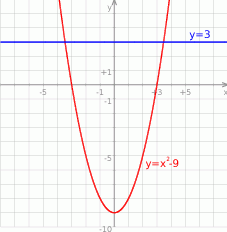
Z rysunku widać, że wykres należy przesunąć do góry wzdłuż osi 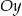 o 12 jednostek. Sprawdźmy jeszcze czy dobrze odczytaliśmy wartości z wykresu. Szukana funkcja będzie przesunięciem funkcji
o 12 jednostek. Sprawdźmy jeszcze czy dobrze odczytaliśmy wartości z wykresu. Szukana funkcja będzie przesunięciem funkcji 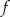 wzdłuż osi
wzdłuż osi 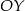 , więc będzie postaci
, więc będzie postaci
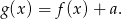
Wierzchołek funkcji 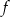 znajduje się w punkcie
znajduje się w punkcie 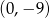 . Musimy tak przesunąć wykres tej funkcji żeby wierzchołek znalazł się w punkcie postaci
. Musimy tak przesunąć wykres tej funkcji żeby wierzchołek znalazł się w punkcie postaci 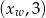 . Zatem
. Zatem
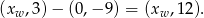
Teraz widać, że trzeba przesunąć o 12 jednostek do góry.
Odpowiedź: B

