/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Okrąg i koło/Pole

Zadanie nr 9707800

Dodaj do ulubionych
Dodaj do rozwiązanych

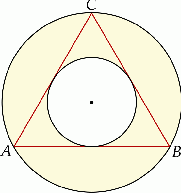
Pole pierścienia kołowego na rysunku jest równe 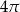4π (mniejszy okrąg jest wpisany w trójkąt 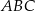ABC , a wierzchołki 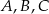A,B ,C leżą na większym okręgu). Zatem długość boku trójkąta równobocznego 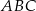ABC jest równa:

PIC

A) 2 B) 4 C) 8 D) 16

Rozwiązanie

Oznaczmy przez R i r promienie odpowiednio większego i mniejszego okręgu, a przez a długość boku trójkąta.

PIC

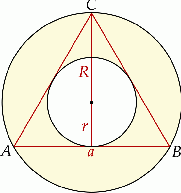
Promień większego okręgu jest równy dwóm trzecim wysokości trójkąta 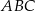ABC , więc

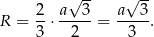
√ -- √ -- 2- a--3- a--3- R = 3 ⋅ 2 = 3 .

Natomiast promień mniejszego okręgu jest równy jednej trzeciej długości wysokości

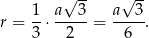
√ -- √ -- 1 a 3 a 3 r = --⋅-----= -----. 3 2 6

Z podanego pola pierścienia mamy

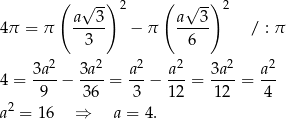
( √ -) 2 ( √ -) 2 4π = π a---3 − π a--3- / : π 3 6 2 2 2 2 2 2 4 = 3a--− 3a--= a--− -a- = 3a--= a-- 9 36 3 1 2 12 4 a2 = 1 6 ⇒ a = 4.

 
Odpowiedź: B

Wersja PDF