/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Monety i banknoty

Zadanie nr 5926883

Rzucamy dziewięć razy symetryczną monetą. Niech 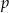p oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
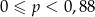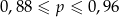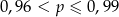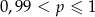
A) 0 ≤ p < 0,88 B) 0,88 ≤ p ≤ 0 ,96 C) 0,96 < p ≤ 0,99 D) 0,99 < p ≤ 1

Wersja PDF

Rozwiązanie

Obliczmy, ile jest zdarzeń elementarnych

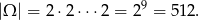
9 |Ω | = 2⋅2 ⋅⋅⋅2 = 2 = 512.

Zauważmy, że jest tylko jedno zdarzenie, w którym jest więcej niż 8 orłów – tak jest, gdy wyrzucimy same reszki. Prawdopodobieństwo jest więc równe

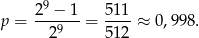
29-−-1- 511- p = 29 = 512 ≈ 0,998.

 
Odpowiedź: D

Wersja PDF