Zadanie nr 6946883
Punkty 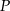 i
i 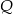 są środkami boków
są środkami boków 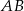 i
i 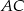 trójkąta
trójkąta 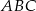 . Bok
. Bok 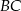 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 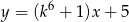 , a punkty
, a punkty 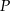 i
i 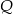 leżą na prostej
leżą na prostej 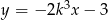 . Wynika stąd, że
. Wynika stąd, że
A) 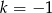 B)
B) 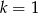 C)
C) 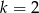 D)
D) 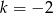
Rozwiązanie
Szkicujemy trójkąt.
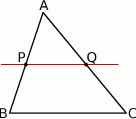
Ponieważ prosta łącząca środki boków w trójkącie jest równoległa do jego podstawy, proste 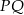 i
i 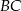 są równoległe. To oznacza, że mają równe współczynniki kierunkowe. Stąd
są równoległe. To oznacza, że mają równe współczynniki kierunkowe. Stąd
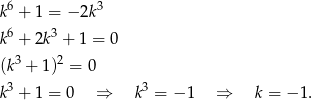
Odpowiedź: A

