Zadanie nr 7352277
Wiadomo, że 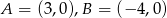 i punkty
i punkty 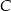 i
i 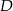 leżą na prostej
leżą na prostej 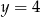 . Pole trójkąta
. Pole trójkąta 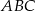 jest równe
jest równe 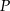 , a pole trójkąta
, a pole trójkąta 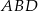 jest równe
jest równe 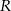 . Zatem
. Zatem
A) 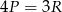 B)
B) 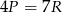 C)
C) 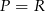 D)
D) 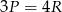
Rozwiązanie
Zaczynamy od szkicowego rysunku
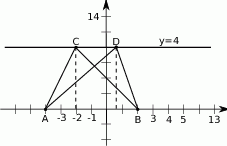
Podstawą trójkąta 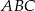 jest odcinek
jest odcinek 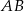 . Podobnie
. Podobnie 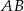 jest podstawą trójkąta
jest podstawą trójkąta 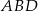 . Zauważmy ponadto, że wysokość opuszczona na podstawę
. Zauważmy ponadto, że wysokość opuszczona na podstawę 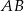 jest w obu przypadkach równa 4. Zatem pola obu trójkątów muszą być równe.
jest w obu przypadkach równa 4. Zatem pola obu trójkątów muszą być równe.
Odpowiedź: C

