/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny/Różne

Zadanie nr 5828955

Dany jest nieskończony rosnący ciąg geometryczny 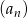(an) o wyrazach dodatnich. Wtedy
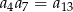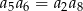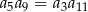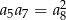
A) a4a7 = a 13 B) a 5a6 = a2a8 C) a a = a a 5 9 3 11 D) a a = a2 5 7 8

Wersja PDF

Rozwiązanie

Sposób I

Równość, o której mowa treści zadania ma zachodzić dla dowolnego ciągu geometrycznego – sprawdźmy więc, która z nich zachodzi dla jednego z najprostszych ciągów geometrycznych, np. 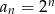an = 2n . Dla tego ciągu spełniona jest tylko równość

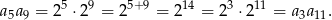
a a = 25 ⋅29 = 25+9 = 214 = 23 ⋅211 = a a . 5 9 3 11

Sposób II

Sprawdzamy kolejne równości korzystając ze wzoru 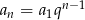an = a1qn− 1 na n -ty wyraz ciągu geometrycznego. Łatwo sprawdzić, że prawdziwa jest tylko równość

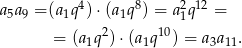
a a = (a q4) ⋅(a q8) = a2q12 = 5 9 1 1 1 = (a1q2) ⋅(a1q10) = a3a11.

 
Odpowiedź: C

Wersja PDF