Zadanie nr 8035480
Wszystkie wyrazy ciągu geometrycznego 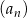 określonego dla
określonego dla 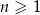 są dodatnie i
są dodatnie i 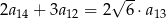 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 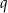 tego ciągu jest równy
tego ciągu jest równy
A) 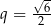 B)
B) 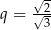 C)
C) 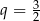 D)
D) 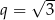
Rozwiązanie
Ze wzoru 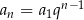 na
na  -ty wyraz ciągu geometrycznego mamy
-ty wyraz ciągu geometrycznego mamy
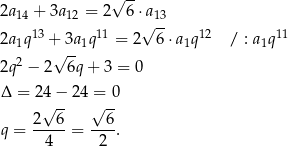
Odpowiedź: A

