Zadanie nr 8927764
Dany jest nieskończony rosnący ciąg geometryczny 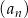 o wyrazach dodatnich. Iloraz
o wyrazach dodatnich. Iloraz 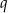 tego ciągu jest jednym z pierwiastków równania kwadratowego
tego ciągu jest jednym z pierwiastków równania kwadratowego 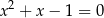 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia
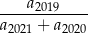
jest równa
A) 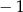 B)
B) 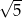 C)
C) 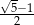 D) 1
D) 1
Rozwiązanie
Korzystamy ze wzoru 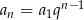 , na
, na  –ty wyraz ciągu geometrycznego. Mamy zatem
–ty wyraz ciągu geometrycznego. Mamy zatem
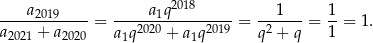
Odpowiedź: D

