Zadanie nr 4057721
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
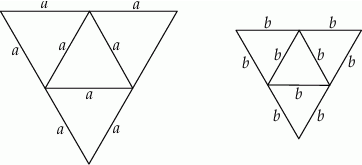
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 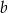 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 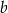 ?
?
A) 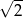 B) 2 C)
B) 2 C) 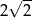 D) 4
D) 4
Rozwiązanie
Obie siatki przedstawiają czworościany foremne (ostrosłupy prawidłowe trójkątne, których ściany boczne są trójkątami równobocznymi).
Jeżeli pole powierzchni pierwszego ostrosłupa jest dwa razy większe od pola powierzchni drugiego ostrosłupa, to znaczy, że są one podobne w skali 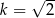 (bo pole zmienia się jak kwadrat skali podobieństwa). Objętość pierwszego ostrosłupa jest więc większa od objętości drugiego
(bo pole zmienia się jak kwadrat skali podobieństwa). Objętość pierwszego ostrosłupa jest więc większa od objętości drugiego
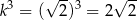
razy (bo objętość zmienia się jak sześcian skali podobieństwa).
Odpowiedź: C

