Zadanie nr 9261100
Przekątna podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości ostrosłupa. Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek jednej z krawędzi bocznych (patrz rysunek).
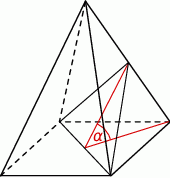
Płaszczyzna przekroju tworzy z podstawą ostrosłupa kąt  o mierze
o mierze
A) 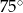 B)
B) 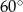 C)
C) 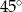 D)
D) 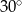
Rozwiązanie
Dorysujmy wysokość ostrosłupa i rzut  środka krawędzi
środka krawędzi  na płaszczyznę podstawy.
na płaszczyznę podstawy.
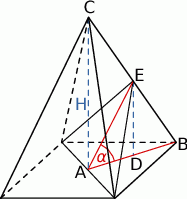
W trójkącie prostokątnym 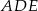 mamy
mamy
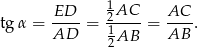
Z założenia 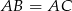 , więc
, więc 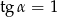 , czyli
, czyli 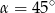 .
.
Odpowiedź: C

