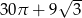/Szkoła podstawowa/Geometria/Okrąg i koło/Pole

Zadanie nr 4790835

Dodaj do ulubionych
Dodaj do rozwiązanych

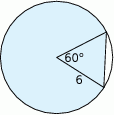
Oblicz pole powierzchni zacieniowanego odcinka koła.

PIC

Rozwiązanie

Interesujące nas pole odcinka koła obliczymy jako sumę pól: wycinka koła wyznaczonego przez kąt środkowy o mierze 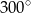30 0∘ , oraz trójkąta równobocznego o boku długości długości 6.

PIC

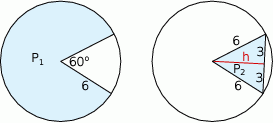
Ponieważ wycinek koła wyznaczony przez kąt o mierze 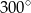300∘ stanowi 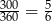330600 = 56 pola koła, jego pole jest równe

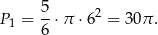
P = 5-⋅π ⋅62 = 30 π. 1 6

Wysokość trójkąta równobocznego o boku długości 6 jest równa

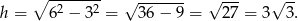
∘ ------- √ ------- √ --- √ -- h = 62 − 32 = 36− 9 = 27 = 3 3.

Pole tego trójkąta jest więc równe

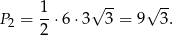
√ -- √ -- P2 = 1-⋅6⋅3 3 = 9 3. 2

W takim razie pole odcinka koła jest równe

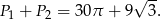
√ -- P1 + P2 = 30 π + 9 3.

 
Odpowiedź: √ -- 30π + 9 3

Wersja PDF