/Studia/Analiza/Zastosowania całek/Pole powierzchni/Płaskie

Zadanie nr 9682484

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole tego obszaru ograniczonego krzywą 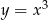3 y = x i parabolą 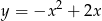y = −x 2 + 2x , który znajduje się w I ćwiartce układu współrzędnych.

Rozwiązanie

Najpierw szukamy punktów, w których te krzywe się przecinają. W tym celu porównujemy ich równania.

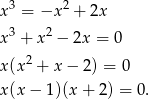
3 2 x = −x + 2x x3 + x2 − 2x = 0 x(x2 + x − 2) = 0 x(x − 1)(x + 2) = 0 .

Zatem krzywe przecinają się w trzech punktach: 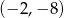(− 2,− 8) , (0,0) i (1,1) .

PIC

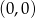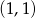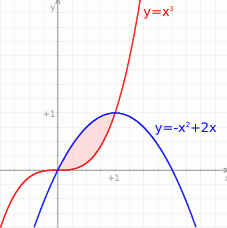
Interesuje nas obszar ograniczony tymi krzywymi i zawarty w pierwszej ćwiartce układu. Jest on opisany nierównościami

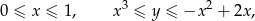
0 ≤ x ≤ 1, x3 ≤ y ≤ −x 2 + 2x ,

a zatem jego pole równa się

∫ 1[ ] [ x 3 x4] 1 −x 2 + 2x − x3 dx = − ---+ x2 − --- = 0 3 4 0 1- 1- −-4-+-12-−-3- -5- = − 3 + 1 − 4 = 12 = 12.

 
Odpowiedź: 152

Wersja PDF