/Szkoła średnia/Równania/Układy równań/Stopnia 2/Różne

Zadanie nr 2411148

Uzasadnij, że nie istnieją dwie liczby rzeczywiste, których suma jest równa 4, a ich iloczyn jest równy 5.

Wersja PDF

Rozwiązanie

Musimy wykazać, że układ równań

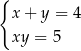
{ x + y = 4 xy = 5

nie ma rozwiązania.

Sposób I

Podstawiamy 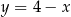y = 4− x z pierwszego równania do drugiego.

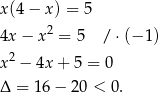
x(4 − x) = 5 2 4x − x = 5 / ⋅(− 1) x2 − 4x + 5 = 0 Δ = 16− 20 < 0.

Ponieważ 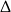Δ jest ujemna, równanie nie ma rozwiązań rzeczywistych.

Sposób II

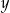Na mocy wzorów Viète’a liczby x i y spełniające dany układ równań są pierwiastkami równania

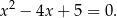
x2 − 4x + 5 = 0 .

To równanie nie ma jednak rozwiązań rzeczywistych (bo 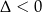Δ < 0 ), więc dany układ równań jest sprzeczny.

Wersja PDF