/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych/Z parametrem

Zadanie nr 4004757

Dodaj do ulubionych
Dodaj do rozwiązanych

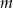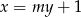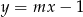Dla jakich wartości parametru m proste x = my + 1 oraz y = mx − 1 przecinają się w jednym punkcie, który leży poniżej prostej x = 1 − 4y ?

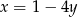Rozwiązanie

Sposób I

Wyznaczmy najpierw punkt wspólny podanych prostych – podstawiamy 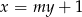x = my + 1 do równania drugiej prostej.

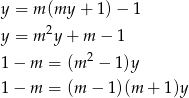
y = m(my + 1) − 1 y = m2y + m − 1 1 − m = (m 2 − 1)y 1 − m = (m − 1)(m + 1 )y

Gdyby 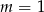m = 1 to powyższe równanie byłoby spełnione przez każdą liczbę 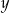y i łatwo sprawdzić wstawiając 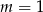m = 1 do równań prostych, że dane proste się wtedy pokrywają. To jednak jest sprzeczne z wymaganiem, aby przecinały się w jednym punkcie. Zatem 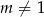m ⁄= 1 i możemy podzielić równanie stronami przez (m − 1) .

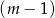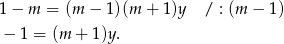
1 − m = (m − 1)(m + 1)y / : (m − 1) − 1 = (m + 1)y .

Jeżeli teraz 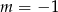m = −1 to równanie jest sprzeczne i dane proste nie mają punktów wspólnych. Musi więc być 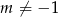m ⁄= −1 . Mamy wtedy

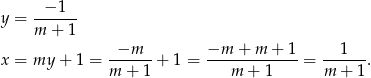
−1 y = ------ m + 1 x = my + 1 = -−m--- + 1 = −m--+-m--+-1-= --1---. m + 1 m + 1 m + 1

Zastanówmy się teraz jak zapisać warunek, że punkt o współrzędnych 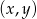(x,y) leży poniżej prostej 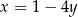x = 1− 4y . Jeżeli zapiszemy równanie tej prostej w postaci

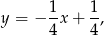
1- 1- y = − 4 x+ 4,

to powinno być jasne, że punkty poniżej tej prostej, to punkty spełniające nierówność

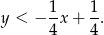
1 1 y < − 4-x+ 4.

Podstawiamy teraz wyliczone wcześniej współrzędne 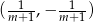(--1-,− --1-) m +1 m +1 .

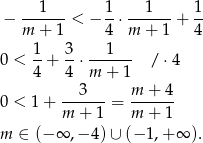
--1--- 1- --1--- 1- − m + 1 < − 4 ⋅ m + 1 + 4 1 3 1 0 < -+ --⋅------ / ⋅4 4 4 m + 1 ---3-- m-+--4 0 < 1 + m + 1 = m + 1 m ∈ (− ∞ ,−4 )∪ (− 1,+ ∞ ).

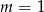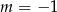Na koniec musimy jeszcze pamiętać o wyrzuceniu punktów m = 1 i m = − 1 , co daje zbiór rozwiązań:

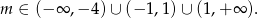
m ∈ (− ∞ ,− 4)∪ (− 1,1 )∪ (1,+ ∞ ).

Sposób II

Punkt wspólny podanych prostych mogliśmy też wyznaczyć używając wyznaczników. Rozwiązujemy układ równań

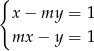
{ x − my = 1 mx − y = 1

Liczymy wyznaczniki

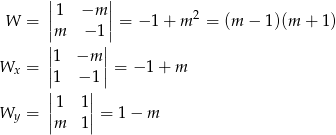
|| 1 −m || W = || || = − 1+ m2 = (m − 1)(m + 1) |m − 1| |1 −m | Wx = ||1 − 1|| = − 1 + m | | || 1 1|| Wy = |m 1| = 1 − m

Widać, że jeżeli 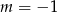m = − 1 to proste nie przecinają się, a jeżeli 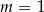m = 1 to proste się pokrywają. Zatem musi być 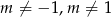m ⁄= −1 ,m ⁄= 1 oraz

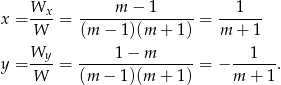
Wx m − 1 1 x = ----= ----------------= ------ W (m − 1)(m + 1) m + 1 Wy-- ----1-−-m------- --1--- y = W = (m − 1)(m + 1) = − m + 1 .

Dalej postępujemy tak samo jak w poprzednim sposobie.  
Odpowiedź: m ∈ (− ∞ ,− 4)∪ (− 1,1) ∪ (1,+ ∞ )

Wersja PDF