/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych/Z parametrem

Zadanie nr 9431297

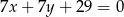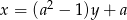Proste 7x + 7y + 2 9 = 0 i 2 x = (a − 1)y + a przecinają się pod kątem 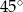∘ 45 . Wyznacz liczbę a .

Wersja PDF

Rozwiązanie

Zauważmy, że współczynnik kierunkowy pierwszej z danych prostych jest równy -1. To oznacza, że jest to prosta równoległa do prostej 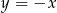y = −x , która jest jedną z dwusiecznych kątów prostych utworzonych przez osie układu współrzędnych.

PIC

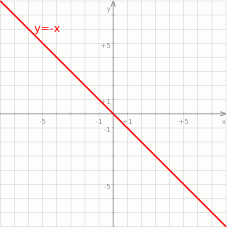
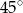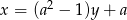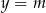Zatem prosta ta tworzy z osiami układu kąty o mierze 45∘ , czyli szukana prosta postaci x = (a2 − 1)y + a musi być pozioma lub pionowa. Nie może być pozioma (bo zawiera x , czyli nie może być postaci y = m ), więc musi być pionowa. Tak będzie, gdy

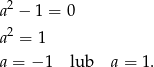
a2 − 1 = 0 a2 = 1 a = − 1 lub a = 1.

 
Odpowiedź: a ∈ {− 1,1 }

Wersja PDF