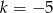/Szkoła średnia/Funkcje - wykresy/Wykładniczy/Rysowanie wykresu

Zadanie nr 5882966

Dana jest funkcja 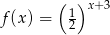( )x+3 f(x ) = 12 , gdzie x ∈ (− 5,0⟩ .

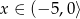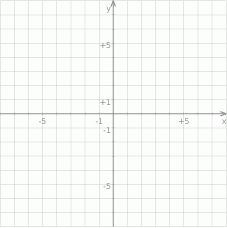
  • Naszkicuj wykres funkcji w układzie współrzędnych.
  • Zapisz za pomocą logarytmu argument, dla którego funkcja 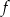f przyjmuje wartość 3. Wiedząc, że argument ten należy do przedziału 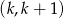(k,k + 1) , gdzie 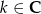k ∈ C , podaj k .
PIC
Wersja PDF

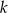Rozwiązanie

  • Wykresem danej funkcji jest fragment wykresu funkcji wykładniczej 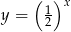( )x y = 1 2 przesuniętego o 3 jednostki w lewo. Żeby wykonać w miarę dokładny szkic wyznaczamy kilka punktów wykresu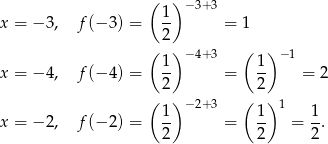
    ( )− 3+3 1- x = −3 , f(− 3) = 2 = 1 ( )− 4+3 ( )− 1 1- 1- x = −4 , f(− 4) = 2 = 2 = 2 ( )− 2+3 ( )1 1- 1- 1- x = −2 , f(− 2) = 2 = 2 = 2.

    Teraz możemy naszkicować wykres.

    PIC
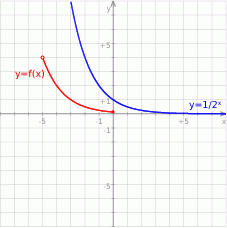
  • Przypomnijmy, że
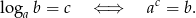
    loga b = c ⇐ ⇒ ac = b.

    Zatem

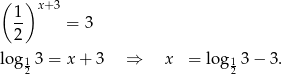
    ( ) 1- x+ 3 2 = 3 log 12 3 = x+ 3 ⇒ x = lo g12 3 − 3.

    Teraz musimy oszacować wartość tej liczby. Funkcja 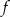f jest malejąca, więc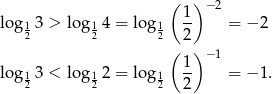

    ( 1) − 2 log 13 > log 14 = log 1 -- = − 2 2 2 2( 2) 1 − 1 log 13 < log 12 = log 1 -- = − 1. 2 2 2 2

    Zatem liczbę x możemy oszacować

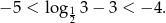
    − 5 < log 12 3 − 3 < − 4.

    To oznacza, że k = − 5 .  
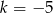    Odpowiedź: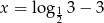 x = log 12 3 − 3 i k = − 5

Wersja PDF