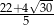Zadanie nr 3871979

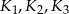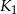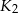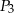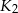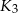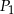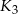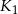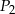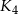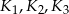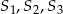Na płaskiej powierzchni położono trzy kule K 1,K2,K 3 , każda o promieniu 2 tak, że kule K 1 i są styczne w punkcie , kule i K 3 są styczne w punkcie , a kule K 3 i są styczne w punkcie . Następnie położono na tych kulach kulę K 4 o promieniu 3, która jest styczna do kul K ,K ,K 1 2 3 odpowiednio w punktach S1,S 2,S 3 .

Uzasadnij, że odcink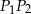i i 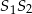są równoległe.
Oblicz obwód trapezu .

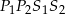Rozwiązanie

Oczywiście rozpoczynamy od narysowania opisanej sytuacji.

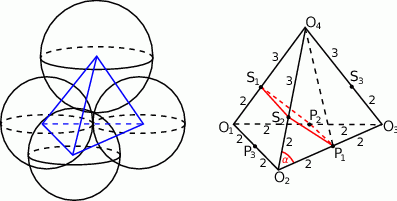
Zrobienie nawet schematycznego rysunku nie jest łatwe, ale musimy sobie co najmniej tyle narysować, żeby było widać, że wystarczy się zajmować czworościanem 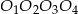O O O O 1 2 3 4 , gdzie punkty te są środkami kolejnych kul. Punkty styczności kul będą dzielić krawędzie tego czworościanu w sposób pokazany na prawym rysunku.

W trójkącie 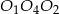mamy
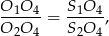
$O-1O-4 S-1O4 O 2O 4 = S 2O4,$

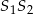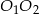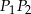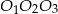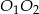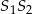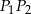co na mocy twierdzenia odwrotnego do twierdzenia Talesa oznacza, że odcinki i są równoległe. Podobnie, odcinek łączy środki boków w trójkącie , czyli jest równoległy do odcinka . Skoro każdy z odcinków i jest równoległy do odcinka 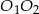, to muszą one być równoległe.
Łatwo wyliczyć długości podstaw trapezu. Z zauważonych w poprzednim podpunkcie równoległości mamy
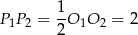
$P P = 1O O = 2 1 2 2 1 2$

oraz

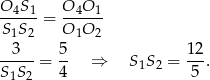
$O 4S1 O 4O1 ----- = ------ S1S2 O 1O2 --3-- 5- 12- S 1S2 = 4 ⇒ S1S 2 = 5 .$

Odrobinę trudniej jest z ramieniem trapezu – widać, że da się wyliczyć długość odcinka 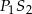z trójkąta 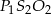jeżeli tylko będziemy znali 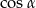. Cosinus ten można wyliczyć z twierdzenia cosinusów w trójkącie 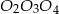, ale można też prościej: trójkąt 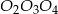jest równoramienny, więc środkowa 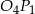jest jego wysokością. Zatem z trójkąta 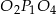mamy

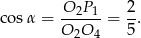
$cos α = O-2P1-= 2-. O 2O 4 5$

Pozostało teraz policzyć długość odcinka 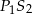z twierdzenia cosinusów w trójkącie .

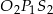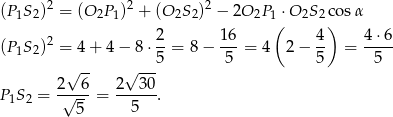
$(P1S2)2 = (O 2P1)2 + (O 2S 2)2 − 2O 2P 1 ⋅O 2S2co sα 2 16 ( 4) 4 ⋅6 (P1S2)2 = 4 + 4 − 8 ⋅--= 8− ---= 4 2− -- = ---- -- --5 5 5 5 2 √ 6 2 √ 30 P1S2 = -√--- = ------. 5 5$

Zatem obwód trapezu jest równy

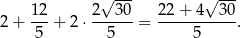
$√ --- √ --- 2 + 12-+ 2⋅ 2--30-= 22+--4--30. 5 5 5$

Odpowiedź: