/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt/Równoległobok

Zadanie nr 6487400

Dodaj do ulubionych
Dodaj do rozwiązanych

Boki równoległoboku są zawarte w prostych o równaniach: 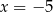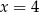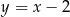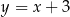x = − 5 , x = 4 , y = x− 2 , y = x + 3 . Pole tego równoległoboku jest równe
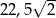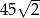A) 45 B) √ -- 22 ,5 2 C) 45 √ 2- D) 22,5

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

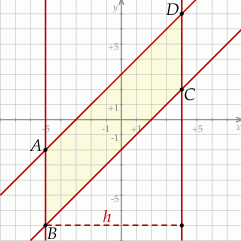
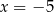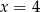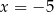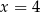Wierzchołki równoległoboku opisanego w treści zadania łatwo wyznaczyć – ich pierwsze współrzędne są równe x = − 5 i x = 4 , a drugie współrzędne otrzymujemy podstawiając x = − 5 i x = 4 w pozostałych dwóch równaniach boków. Gdy to zrobimy otrzymamy punkty

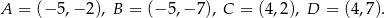
A = (− 5,− 2), B = (− 5,− 7), C = (4,2), D = (4,7).

Widać teraz, że podstawa równoległoboku ma długość 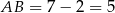AB = 7− 2 = 5 , a wysokość jest równa 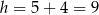h = 5 + 4 = 9 . Pole tego równoległoboku jest więc równe

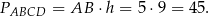
PABCD = AB ⋅h = 5 ⋅9 = 45.

 
Odpowiedź: A

Wersja PDF