/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt/Równoległobok

Zadanie nr 8196734

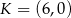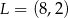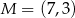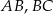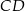Punkty K = (6,0) , L = (8,2) i M = (7,3) to środki boków, odpowiednio AB ,BC i CD równoległoboku 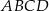ABCD . Różnica długości przekątnych tego równoległoboku jest równa
A) 4 B) 2 C) 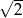√ 2- D) √ -- 2 2

Wersja PDF

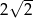
Rozwiązanie

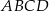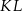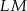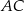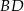Jeżeli narysujemy (lub przynajmniej wyobrazimy) sobie równoległobok ABCD , to widać, że długości odcinków KL i LM są dwa razy mniejsze od długości przekątnych AC i BD równoległoboku (są to odcinki łączące środki boków w trójkątach 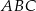ABC i BCD ).

PIC

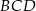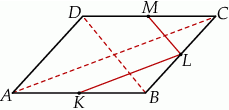
Mamy zatem

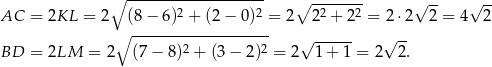
∘ ------------------- ∘ ------- √ -- √ -- AC = 2KL = 2 (8− 6 )2 + (2 − 0)2 = 2 22 + 22 = 2 ⋅2 2 = 4 2 ∘ ------------------- √ ------ √ -- BD = 2LM = 2 (7 − 8)2 + (3 − 2)2 = 2 1 + 1 = 2 2.

Różnica długości przekątnych jest więc równa

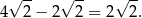
√ -- √ -- √ -- 4 2 − 2 2 = 2 2.

 
Odpowiedź: D

Wersja PDF