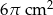Zadanie nr 7005849
W wycinek koła o kącie 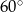 wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
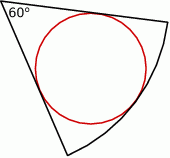
Rozwiązanie
Sposób I
Zaznaczmy środek wpisanego okręgu i połączmy go z punktami styczności.
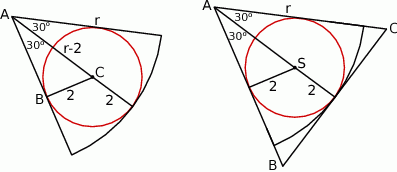
Utworzony trójkąt 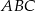 jest prostokątny oraz
jest prostokątny oraz 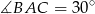 (bo
(bo 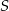 leży na dwusiecznej kąta o wierzchołku
leży na dwusiecznej kąta o wierzchołku 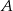 ). Jest to więc połówka trójkąta równobocznego i
). Jest to więc połówka trójkąta równobocznego i
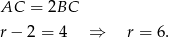
W takim razie pole wycinka jest równe
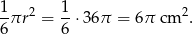
Sposób II
Tym razem dorysujmy wspólną styczną do wycinka i okręgu wpisanego w wycinek. Przedłużając promienie wycinka otrzymujemy w ten sposób trójkąt równoboczny 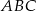 , w którym promień okręgu wpisanego ma długość 2. Wysokość
, w którym promień okręgu wpisanego ma długość 2. Wysokość  tego trójkąta spełnia więc warunek
tego trójkąta spełnia więc warunek
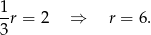
W takim razie pole wycinka jest równe
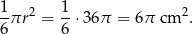
Odpowiedź: