/Szkoła średnia/Zadania maturalne/Matura 2011
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 2 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczba 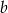 jest 3 razy większa od liczby
jest 3 razy większa od liczby  . Wtedy
. Wtedy
A) 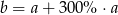 B)
B) 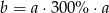 C)
C) 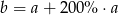 D)
D) 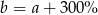
Liczba 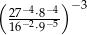 jest równa
jest równa
A) 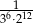 B)
B) 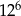 C)
C) 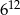 D)
D) 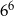
Rozwiązaniem nierówności 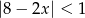 jest zbiór
jest zbiór
A) 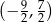 B)
B) 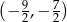 C)
C) 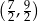 D)
D) 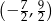
Liczba 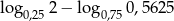 jest równa
jest równa
A)  B) 4 C)
B) 4 C) 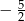 D) 0
D) 0
Wyrażenie 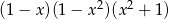 jest równe
jest równe
A) 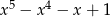 B)
B) 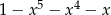 C)
C) 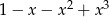 D)
D) 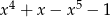
Ciąg 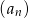 określony jest wzorem
określony jest wzorem 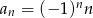 , gdzie
, gdzie 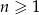 . Wówczas wyrażenie
. Wówczas wyrażenie 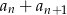 jest równe
jest równe
A) 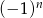 B)
B) 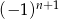 C)
C) 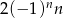 D)
D) 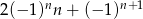
Zbiorem wartości funkcji 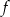 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
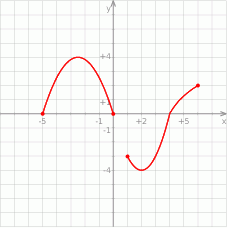
A) 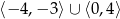 B)
B) 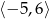 C)
C) 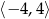 D)
D) 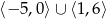
Wykresem funkcji kwadratowej 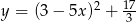 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 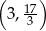 B)
B) 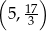 C)
C) 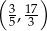 D)
D) 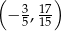
Do zbioru rozwiązań nierówności 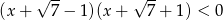 należy liczba
należy liczba
A) 0 B) -3 C) -1 D) 3
Pole rombu jest równe 25, a jedna z jego przekątnych jest 2 razy dłuższa od drugiej. Suma długości przekątnych jest równa
A) 15 B) 5 C) 10 D) 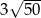
Do wykresu funkcji 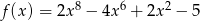 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 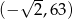 B)
B) 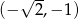 C)
C) 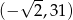 D)
D) 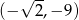
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
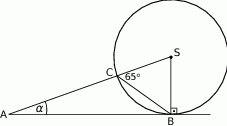
A) 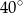 B)
B) 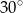 C)
C) 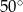 D)
D) 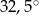
Kąt  jest ostry i
jest ostry i 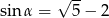 . Wartość wyrażenia
. Wartość wyrażenia 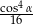 jest równa
jest równa
A) 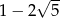 B)
B) 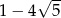 C)
C) 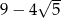 D)
D) 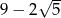
W ciągu arytmetycznym mamy 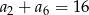 . Oblicz
. Oblicz 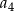 .
.
A) 8 B) 16 C) 4 D) 12
Punkty 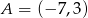 i
i 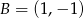 są wierzchołkami pięciokąta foremnego
są wierzchołkami pięciokąta foremnego 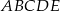 . Obwód tego pięciokąta jest równy
. Obwód tego pięciokąta jest równy
A) 50 B) 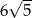 C) 60 D)
C) 60 D) 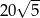
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 7, a krawędź podstawy ma długość 8. Wysokość tego ostrosłupa jest równa
A) 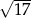 B)
B) 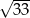 C) 9 D) 5
C) 9 D) 5
Równanie 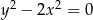 opisuje na płaszczyźnie
opisuje na płaszczyźnie
A) parabolę
B) dwie proste równoległe
C) dwie proste prostopadłe
D) dwie proste przecinające się pod kątem innym niż prosty
Przekątna 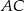 prostokąta
prostokąta 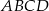 ma długość
ma długość 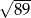 , a bok
, a bok 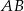 jest o 3 dłuższy od boku
jest o 3 dłuższy od boku 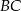 . Oblicz pole prostokąta.
. Oblicz pole prostokąta.
A) 8 B) 40 C) 5 D) 20
Do okręgu o środku 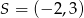 i promieniu
i promieniu 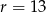 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 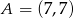 B)
B) 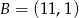 C)
C) 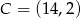 D)
D) 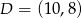
Stosunek pól powierzchni dwóch kul jest równy 1:4. Wobec tego stosunek objętości tych kul jest równy
A) 1:2 B) 1:8 C) 1:4 D) 1:16
Liczba ujemnych wyrazów ciągu 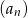 określonego wzorem
określonego wzorem 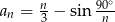 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Punkty 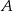 oraz
oraz 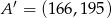 są symetryczne względem prostej
są symetryczne względem prostej 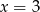 . Wówczas
. Wówczas
A) 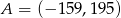 B)
B) 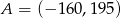 C)
C) 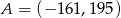 D)
D) 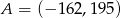
Pole powierzchni całkowitej czworościanu foremnego jest równe 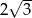 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 12 B) 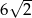 C)
C) 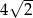 D)
D) 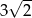
Ze zbioru liczb naturalnych zawartych w przedziale 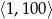 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 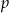 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
A) 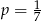 B)
B) 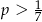 C)
C) 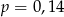 D)
D) 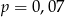
Zadania otwarte
Rozwiąż nierówność 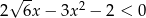 .
.
Rozwiąż równanie 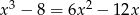 .
.
Wyznacz równanie okręgu opisanego na prostokącie 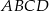 , w którym
, w którym 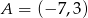 i
i 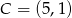 .
.
Iloczyn  początkowych wyrazów ciągu geometrycznego wyraża się wzorem
początkowych wyrazów ciągu geometrycznego wyraża się wzorem 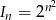 . Oblicz pierwszy wyraz tego ciągu i jego iloraz.
. Oblicz pierwszy wyraz tego ciągu i jego iloraz.
Uzasadnij, że jeśli 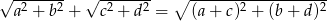 to
to 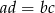 .
.
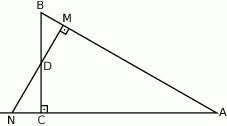
Przez środek 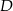 przyprostokątnej
przyprostokątnej 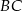 trójkąta prostokątnego
trójkąta prostokątnego 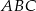 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 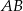 . Prosta ta przecina proste
. Prosta ta przecina proste 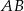 i
i 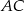 odpowiednio w punktach
odpowiednio w punktach 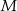 i
i 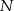 . Wykaż, że
. Wykaż, że 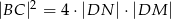 .
.
Podstawą ostrosłupa 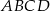 jest trójkąt
jest trójkąt 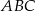 . Krawędź
. Krawędź 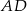 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
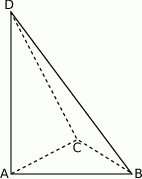
Oblicz objętość ostrosłupa 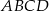 , jeśli wiadomo, że
, jeśli wiadomo, że 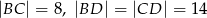 oraz pole podstawy jest równe 24.
oraz pole podstawy jest równe 24.
Antek zatrudnił się przy zbiórce truskawek. Każdego dnia zbiera taką samą liczbę kilogramów owoców i w sumie uzbierał 96 kilogramów. Gdyby każdego dnia zbierał o 4 kilogramy więcej, to tę samą ilość owoców uzbierałby w czasie krótszym o cztery dni. Oblicz, ile kilogramów owoców zbierał Antek każdego dnia i w ciągu ilu dni je zebrał.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 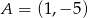 oraz
oraz 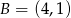 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 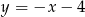 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.

