/Szkoła średnia/Zadania maturalne/Matura 2011
Egzamin Maturalny
z Matematyki poziom podstawowy 5 maja 2011 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, którą spełnia liczba 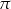 .
.
A) 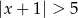 B)
B) 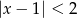 C)
C) 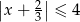 D)
D) 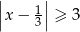
Pierwsza rata, która stanowi 9% ceny roweru, jest równa 189 zł. Rower kosztuje
A) 1701 zł B) 2100 zł C) 1890 zł D) 2091 zł
Wyrażenie 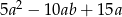 jest równe iloczynowi
jest równe iloczynowi
A) 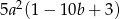 B)
B) 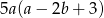 C)
C) 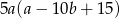 D)
D) 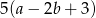
Układ równań 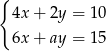 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 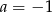 B)
B) 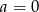 C)
C) 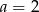 D)
D) 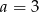
Rozwiązanie równania 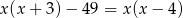 należy do przedziału
należy do przedziału
A) 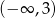 B)
B) 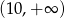 C)
C) 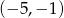 D)
D) 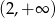
Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności 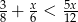 jest
jest
A) 1 B) 2 C) 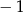 D)
D) 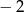
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: 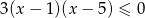 i
i 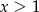 .
.

Wyrażenie 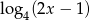 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 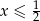 B)
B) 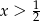 C)
C) 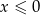 D)
D) 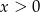
Dane są funkcje liniowe 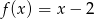 oraz
oraz 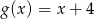 określone dla wszystkich liczb rzeczywistych
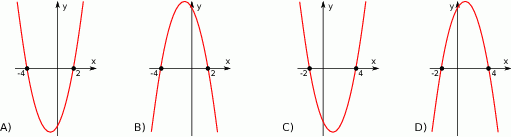
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 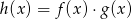 .
.
Funkcja liniowa określona jest wzorem 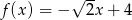 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 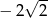 B)
B) 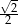 C)
C) 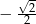 D)
D) 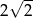
Dany jest nieskończony ciąg geometryczny 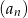 , w którym
, w którym 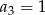 i
i 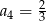 . Wtedy
. Wtedy
A) 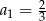 B)
B) 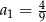 C)
C) 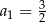 D)
D) 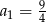
Dany jest nieskończony rosnący ciąg arytmetyczny 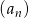 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 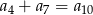 B)
B) 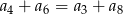 C)
C) 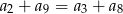 D)
D) 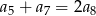
Kąt  jest ostry i
jest ostry i 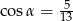 . Wtedy
. Wtedy
A) 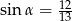 oraz
oraz 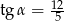
B) 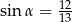 oraz
oraz 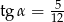
C) 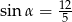 oraz
oraz 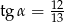
D) 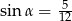 oraz
oraz 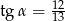
Wartość wyrażenia 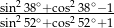 jest równa
jest równa
A) 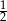 B) 0 C)
B) 0 C) 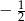 D) 1
D) 1
W prostopadłościanie 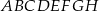 mamy:
mamy: 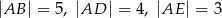 . Który z odcinków
. Który z odcinków 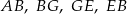 jest najdłuższy?
jest najdłuższy?
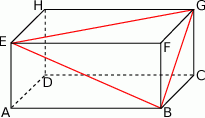
A) 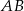 B)
B) 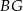 C)
C) 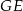 D)
D) 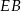
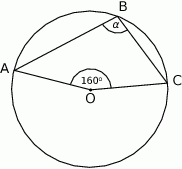
Punkt 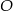 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 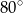 B)
B) 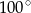 C)
C) 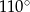 D)
D) 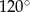
Wysokość rombu o boku długości 6 i kącie ostrym 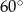 jest równa
jest równa
A) 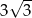 B) 3 C)
B) 3 C) 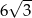 D) 6
D) 6
Prosta 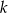 ma równanie
ma równanie 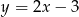 . Wskaż równanie prostej
. Wskaż równanie prostej 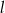 równoległej do prostej
równoległej do prostej 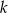 i przechodzącej przez punkt
i przechodzącej przez punkt 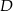 o współrzędnych
o współrzędnych 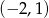 .
.
A) 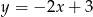 B)
B) 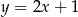 C)
C) 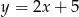 D)
D) 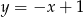
Styczną do okręgu 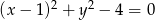 jest prosta o równaniu
jest prosta o równaniu
A) 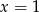 B)
B) 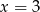 C)
C) 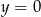 D)
D) 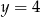
Pole powierzchni całkowitej sześcianu jest równe 54. Długość przekątnej tego sześcianu jest równa
A) 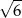 B) 3 C) 9 D)
B) 3 C) 9 D) 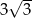
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 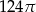 B)
B) 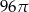 C)
C) 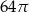 D)
D) 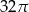
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
A) 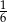 B)
B) 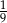 C)
C) 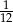 D)
D) 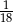
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja rodzina?” Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba uczniów |
| 3 | 6 |
| 4 | 12 |
| x | 2 |
Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa
A) 3 B) 4 C) 5 D) 7
Zadania otwarte
Rozwiąż nierówność 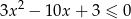 .
.
Uzasadnij, że jeżeli 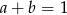 i
i 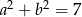 , to
, to 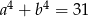 .
.
Na rysunku przedstawiono wykres funkcji 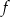 .
.
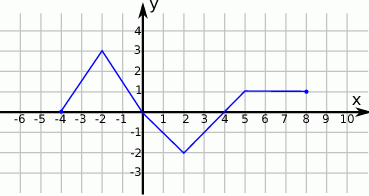
Odczytaj z wykresu i zapisz:
- zbiór wartości funkcji
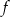 ,
, - przedział maksymalnej długości, w którym funkcja
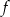 jest malejąca.
jest malejąca.
Liczby 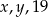 w podanej kolejności tworzą ciąg arytmetyczny, przy czym
w podanej kolejności tworzą ciąg arytmetyczny, przy czym 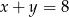 . Oblicz
. Oblicz  i
i 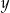 .
.
Kąt  jest ostry i
jest ostry i 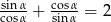 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 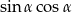 .
.
Dany jest czworokąt 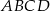 , w którym
, w którym 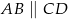 . Na boku
. Na boku 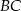 wybrano taki punkt
wybrano taki punkt 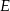 , że
, że 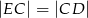 i
i 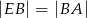 . Wykaż, że kąt
. Wykaż, że kąt 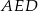 jest prosty.
jest prosty.
Ze zbioru liczb 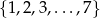 losujemy kolejno dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.
losujemy kolejno dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.
Okrąg o środku w punkcie 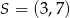 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 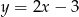 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Pewien turysta pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów. Gdyby mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby przechodzić o 12 km mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.
Punkty 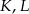 i
i 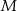 są środkami krawędzi
są środkami krawędzi 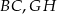 i
i 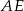 sześcianu
sześcianu 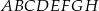 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 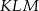 .
.