/Szkoła średnia/Zadania maturalne/Matura 2011
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 2 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Motor kosztował 4500 zł. Jego cenę obniżono o 10%, a następnie cenę po tej obniżce ponownie obniżono o 10%. Po tych obniżkach motor kosztował
A) 3660 zł B) 3705 zł C) 3645 zł D) 3600 zł
Iloraz 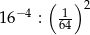 jest równy
jest równy
A) 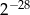 B)
B) 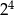 C)
C) 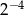 D)
D) 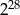
Stosunek pól dwóch kół jest równy 16. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) o 16 B) o 4 C) 4 razy D) 16 razy
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 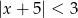 B)
B) 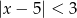 C)
C) 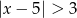 D)
D) 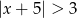
Która z liczb jest równa 2?
A) 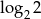 B)
B) 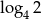 C)
C) 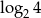 D)
D) 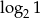
Iloczyn wielomianów 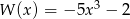 i
i 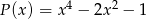 jest wielomianem stopnia
jest wielomianem stopnia
A) 7 B) 3 C) 5 D) 6
Ile rozwiązań rzeczywistych ma równanie 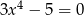 ?
?
A) 4 B) 3 C) 2 D) 1
Do wykresu funkcji 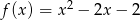 należy punkt
należy punkt
A) 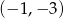 B)
B) 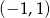 C)
C) 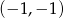 D)
D) 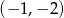
Wierzchołek paraboli 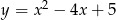 leży na prostej o równaniu
leży na prostej o równaniu
A) 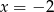 B)
B) 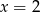 C)
C) 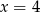 D)
D) 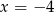
Maksymalny przedział, w którym funkcja 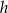 (rysunek poniżej)
(rysunek poniżej)
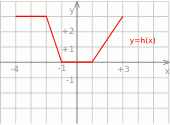
jest malejąca to
A) 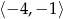 B)
B) 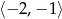 C)
C) 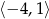 D)
D) 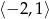
Funkcja 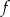 określona jest wzorem
określona jest wzorem
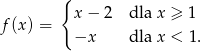
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
W malejącym ciągu geometrycznym 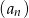 mamy:
mamy: 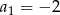 i
i 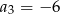 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 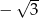 B)
B) 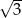 C) -3 D) 3
C) -3 D) 3
Punkt 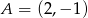 jest początkiem odcinka
jest początkiem odcinka 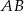 , gdzie
, gdzie 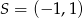 jest jego środkiem. Punkt
jest jego środkiem. Punkt 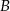 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 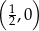 B)
B) 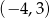 C)
C) 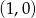 D)
D) 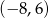
Dany jest okrąg o równaniu 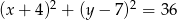 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 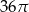 B)
B) 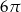 C)
C) 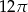 D)
D) 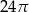
Pionowy słupek o wysokości 60 cm rzuca cień o długości 90 cm. W tej samej chwili stojąca obok wieża rzuca cień długości 12 m. Jaka jest wysokość wieży?
A) 18 m B) 8 m C) 9 m D) 16 m
Kąt  jest ostry i
jest ostry i 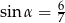 . Wówczas
. Wówczas 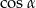 jest równy
jest równy
A) 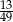 B)
B) 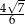 C)
C) 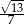 D)
D) 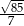
Dany jest trójkąt prostokątny (patrz rysunek).
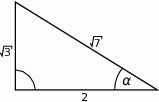
Wtedy 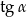 jest równy
jest równy
A) 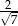 B)
B) 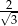 C)
C) 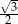 D)
D) 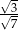
Punkty 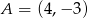 i
i 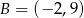 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 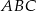 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 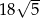 B)
B) 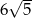 C) 45 D) 54
C) 45 D) 54
Punkty 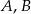 i
i 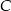 leżą na okręgu o środku
leżą na okręgu o środku 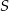 (zobacz rysunek).
(zobacz rysunek).
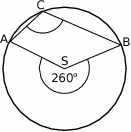
Miara zaznaczonego kąta wpisanego 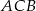 jest równa
jest równa
A) 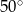 B)
B) 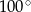 C)
C) 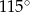 D)
D) 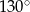
Które z równań opisuje prostą prostopadłą do prostej o równaniu 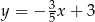 ?
?
A) 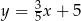 B)
B) 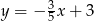 C)
C) 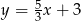 D)
D) 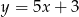
O zdarzeniach losowych 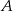 i
i 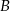 zawartych w
zawartych w 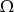 wiadomo, że
wiadomo, że 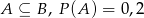 i
i 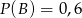 . Wtedy
. Wtedy
A) 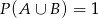 B)
B) 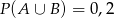 C)
C) 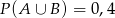 D)
D) 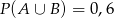
Pan Łukasz ma 3 marynarki, 8 par różnych spodni i 11 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 22 C) 132 D) 264
Powierzchnia sześcianu wynosi 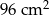 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Liczba ujemnych wyrazów ciągu 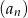 określonego wzorem
określonego wzorem 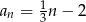 , gdzie
, gdzie 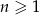 jest równa
jest równa
A) 6 B) 5 C) 9 D) 7
Średnia arytmetyczna dziesięciu liczb 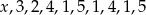 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 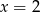 B)
B) 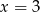 C)
C) 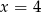 D)
D) 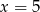
Zadania otwarte
Rozwiąż nierówność 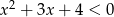 .
.
Uzasadnij, że jeśli 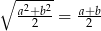 to
to 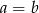 .
.
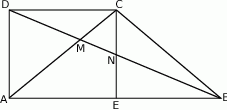
Punkt 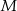 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 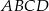 . Punkt
. Punkt 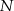 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 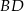 i wysokości
i wysokości 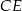 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 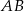 . Wykaż, że
. Wykaż, że 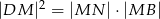 .
.
Wykaż, że trójkąt 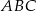 o wierzchołkach
o wierzchołkach 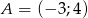 ,
, 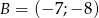 ,
, 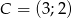 jest prostokątny.
jest prostokątny.
Rozwiąż równanie 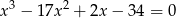 .
.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 6.
Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 6. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 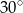 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

