/Gimnazjum/Egzamin gimnazjalny/Egzamin 2012
Próbny Egzamin Gimazjalny
z Matematyki Informator CKE
Liczbę 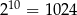 możemy przybliżyć tak:
możemy przybliżyć tak: 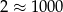 , a liczbę
, a liczbę 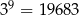 tak:
tak: 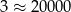 . To pozwala przybliżać inne liczby, na przykład
. To pozwala przybliżać inne liczby, na przykład 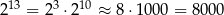 .
.
Wykorzystując podane przybliżenia liczb 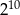 oraz
oraz 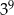 , wybierz najlepsze przybliżenie liczb
, wybierz najlepsze przybliżenie liczb 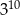 ,
, 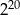 oraz
oraz 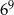 .
.
| Potęga | Propozycje przybliżeń | ||
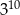 | A) 30 000 | B) 60 000 | C) 200 000 |
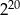 | A) 2 000 | B) 4 000 | C) 1 000 000 |
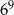 | A) 15 000 | B) 40 000 | C) 10 000 000 |
VAT to podatek doliczany do cen towarów i usług. Cena powiększona o doliczony podatek VAT nazywana jest ceną brutto. W pewnym sklepie stawka VAT na wszystkie towary wynosi 22%. Jeśli znamy cenę brutto towaru z tego sklepu, to aby obliczyć jego cenę bez podatku, wystarczy
| od ceny brutto odjąć jej 22% | P | F |
| podzielić cenę brutto przez 1,22 | P | F |
| obliczyć 78% ceny brutto | P | F |
| pomnożyć cenę brutto przez 100 i wynik podzielić przez 122 | P | F |
| podzielić cenę brutto przez 0,78 | P | F |
Uczestnicy turnieju szachowego rozgrywali partie według zasady „każdy z każdym”. Uzupełnij tabelę.
| Liczba uczestników turnieju | Liczba wszystkich partii rozegranych przez jednego uczestnika | Liczba wszystkich partii rozegranych w turnieju |
| 2 | 1 | 1 |
| 3 | 2 | 3 |
| 4 | 3 | 6 |
| 5 | 4 | |
| 10 | 45 | |
| 21 | 20 | |
 | 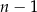 |
Wyobraź sobie, że układasz rzędami guziki żółte (ż) i białe (b) według reguły przedstawionej na schemacie:
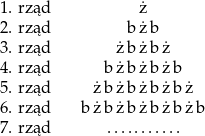
W kolejnym rzędzie najpierw układasz guziki tak, jak w poprzednim rzędzie, a potem dokładasz na obu końcach po jednym guziku, dbając o to, by sąsiednie guziki w rzędzie różniły się kolorami.
Uzupełnij zdania.
A) W 6. rzędzie jest . . . . . . guzików, w tym . . . . . . białych i . . . . . . żółtych.
B) W 7. rzędzie będzie . . . . . . guzików, w tym . . . . . . białych i . . . . . . żółtych.
C) W 100. rzędzie będzie . . . . . . białych i . . . . . . żółtych guzików.
D) W 101. rzędzie będzie . . . . . . białych i . . . . . . żółtych guzików.
E) Jeśli  jest liczbą parzystą, to w rzędzie o numerze
jest liczbą parzystą, to w rzędzie o numerze  będzie . . . . . . białych i . . . . . . żółtych guzików.
będzie . . . . . . białych i . . . . . . żółtych guzików.
Kod dostępu do komputera Andrzeja złożony jest z czterech kolejnych wielokrotności liczby 7 ustawionych od najmniejszej do największej. Suma tych wielokrotności wynosi 294. Znajdź liczby, z których złożony jest ten kod. Zapisz swoje rozumowanie.
Informacja do zadań 6 i 7
Ze zbiornika I, w którym znajdowało się 100 litrów wody, przelewano wodę do zbiornika II. Na wykresie przedstawiono, jak zmieniała się objętość wody w zbiorniku II od chwili, w której rozpoczęto przelewanie ze zbiornika I.
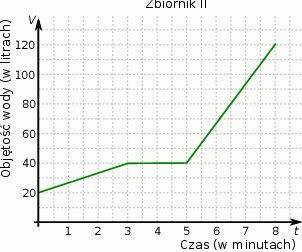
Uzupełnij zdania.
W chwili rozpoczęcia przelewania w zbiorniku II znajdowało się . . . . . . . . . litrów wody.
W ciągu pierwszych trzech minut ze zbiornika I do zbiornika II przelano . . . . . . . . litrów wody, a w ciągu pierwszych pięciu minut przelano . . . . . . . . . litrów.
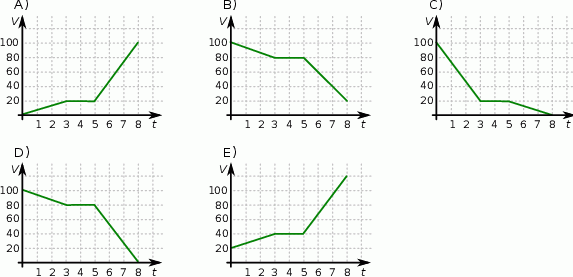
Na którym z poniższych wykresów przedstawiono, jak zmieniała się objętość wody w zbiorniku I w czasie przelewania?
W pudełku znajduje się 30 losów loterii. 5 z tych losów jest wygrywających, 10 jest przegrywających, a wyciągnięcie jednego z pozostałych upoważnia do wyciągnięcia jeszcze jednego losu. Po wyciągnięciu los nie jest zwracany do pudełka. Pierwsza osoba, która brała udział w tej loterii, wyciągnęła los przegrywający.
Czy podane zdania są prawdziwe (P), czy fałszywe (F)? Zaznacz właściwą odpowiedź.
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu wygrywającego wzrosło. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu przegrywającego zmalało. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu upoważniającego do ponownego losowania nie zmieniło się. | P | F |
W koszu znajduje się 6 jabłek zielonych, 8 czerwonych i 4 żółte. Joasia z zawiązanymi oczami wyjmuje jabłka z kosza. Ile co najmniej jabłek powinna wyjąć, aby mieć pewność, że wyjęła przynajmniej jedno czerwone jabłko?
A) 8 B) 10 C) 11 D) 17
Równoległobok, w którym stosunek długości sąsiednich boków wynosi 2:3, podzielono wzdłuż przekątnej o długości 13 cm na dwa przystające trójkąty. Obwód każdego z tych trójkątów jest równy 33 cm. Czy podane zdania są prawdziwe? Zaznacz właściwą odpowiedź.
| Równoległobok ma obwód 40 cm. | P | F |
| Równoległobok ma bok o długości 12 cm. | P | F |
| Jeden z boków równoległoboku jest dwa razy krótszy od drugiego. | P | F |
Ponumeruj poniższe czynności od 1 do 4 według kolejności prowadzącej do skonstruowania symetralnej odcinka 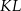 .
.
. . . . . Kreślimy okręgi o promieniu  i środkach w
i środkach w 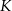 i
i 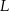 .
.
. . . . . Prowadzimy prostą przechodzącą przez punkty wspólne okręgów.
. . . . . Wybieramy odcinek  większy od połowy długości odcinka
większy od połowy długości odcinka 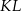 .
.
. . . . . Wyznaczamy punkty wspólne okręgów.
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?
Uzasadnij, że oba kąty przy podstawie 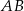 trójkąta
trójkąta 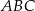 są równe.
są równe.
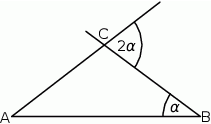
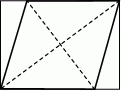
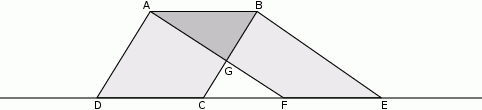
Na rysunku przedstawiono dwa równoległoboki 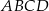 i
i 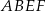 . Uzasadnij, że czworokąty
. Uzasadnij, że czworokąty 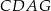 oraz
oraz 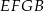 mają równe pola.
mają równe pola.
Puszki z przecierem pomidorowym mają kształt walca o średnicy podstawy 4 cm oraz wysokości 3 cm. Puszki te mogą być na kilka sposobów zapakowane ciasno po 4 sztuki w prostopadłościenne tekturowe pudełka. Wybierz jeden z możliwych sposobów zapakowania puszek, zrób odręczny rysunek siatki odpowiedniego prostopadłościanu i podaj długości krawędzi tego prostopadłościanu.
Każdy z dwóch jednakowych sześcianów o krawędzi 2 cm podzielono na mniejsze sześciany o krawędzi 1 cm. Czy z otrzymanych w ten sposób małych sześciennych kostek można ułożyć jeden pełny sześcian, tak by wszystkie kostki były wykorzystane? Wybierz odpowiedź T lub N i jej uzasadnienie wybrane spośród A, B, C, D.
| Tak | Nie |
| ponieważ | |
| A) | Liczba małych kostek nie jest podzielna przez 3. |
| B) | Liczba małych kostek jest potęgą liczby 2. |
| C) | Liczba małych kostek jest drugą potęgą liczby naturalnej. |
| D) | Liczba małych kostek nie jest trzecią potęgą liczby naturalnej. |
Z jednakowych sześciennych kostek, których krawędź ma długość 1, sklejono bryłę przedstawioną na rysunku.
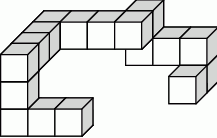
Ile kostek należy dokleić do tej bryły, aby otrzymać wypełniony kostkami sześcian?
Z kartonu wykonano modele sześcianu i graniastosłupa prawidłowego czworokątnego. Podstawa sześcianu jest taka sama jak podstawa graniastosłupa. Na wykonanie sześcianu zużyto 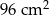 kartonu, a na graniastosłup o
kartonu, a na graniastosłup o 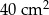 więcej (nie wliczając powierzchni zakładek).
więcej (nie wliczając powierzchni zakładek).
Korzystając z powyższych informacji, oceń prawdziwość poniższych zdań (P – prawda, F – fałsz).
Na wykonanie jednej ściany sześcianu zużyto 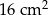 kartonu. kartonu. | P | F |
| Podstawą każdej z tych brył jest kwadrat o boku 4 cm. | P | F |
Pole powierzchni bocznej graniastosłupa jest równe 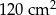 . . | P | F |
| Wysokość graniastosłupa jest równa 6 cm. | P | F |
Poczta przyjmuje do wysłania tylko te paczki, których wymiary spełniają określone warunki. Jeśli paczka ma kształt prostopadłościanu, to spełnione muszą być następujące trzy warunki:
a) najdłuższa krawędź (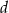 ) tego prostopadłościanu nie może przekraczać 150 cm
) tego prostopadłościanu nie może przekraczać 150 cm
b) suma długości 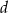 i obwodu ściany ograniczonej krótszymi krawędziami nie może przekraczać 300 cm
i obwodu ściany ograniczonej krótszymi krawędziami nie może przekraczać 300 cm
c) jedna ze ścian paczki (przeznaczona do naklejenia adresu) musi mieć wymiary co najmniej 14 cm na 9 cm.

Przygotowano paczki o wymiarach
I: 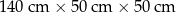
II: 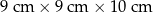
III: 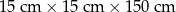
Uzupełnij tabelę
| Nr paczki | Czy paczka zostanie przyjęta do wysłania? Wpisz TAK lub NIE | Jeśli paczka nie zostanie przyjęta do wysłania, podaj warunek, który nie został spełniony. Wpisz literę a, b lub c |
| I | ||
| II | ||
| III |
Stożek o wysokości 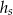 i walec o wysokości
i walec o wysokości 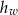 mają takie same podstawy o polu
mają takie same podstawy o polu 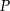 . Stożek ma dwa razy większą objętość niż walec, czyli
. Stożek ma dwa razy większą objętość niż walec, czyli 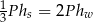 .
.
Zależność między wysokością stożka a wysokością walca można zapisać za pomocą równości
A) 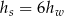 B)
B) 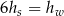 C)
C) 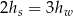 D)
D)