/Gimnazjum/Egzamin gimnazjalny/Egzamin 2012
Próbny Egzamin Gimnazjalny
z Matematyki CKE październik 2011 Czas pracy: 90 minut
Do przygotowania podwieczorku użyto 120 mandarynek i 180 śliwek. Każda porcja składała się z takiej samej liczby mandarynek i takiej samej liczby śliwek, a owoców nie dzielono na części.
Dla ilu maksymalnie osób przygotowano taki podwieczorek? Wybierz odpowiedź spośród podanych.
A) 90 B) 20 C) 30 D) 60
Informacja do zadań 2 i 3
Asia trenuje kolarstwo. Trasa, którą pokonała w ciągu 4 godzin, wiodła leśną drogą, ścieżką rowerową, a następnie polną drogą i chodnikiem. Na diagramie przedstawiono w procentach czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją dotyczącą jazdy po chodniku.
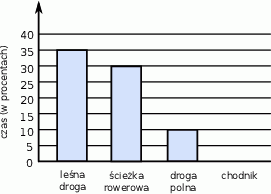
Jaki procent czasu Asia jechała po chodniku? Wybierz odpowiedź spośród podanych.
A) 10% B) 15% C) 20% D) 25%
Ile minut Asia jechała leśną drogą? Wybierz odpowiedź spośród podanych.
A) 60 minut B) 72 minuty C) 84 minuty D) 96 minut
Korzystając z tego, że 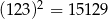 , wskaż wartość liczby
, wskaż wartość liczby 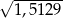 .
.
Zaznacz dobrą odpowiedź.
A) 0,0123 B) 0,123 C) 1,23 D) 12,3
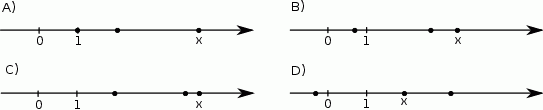
Na rysunkach przedstawiono osie liczbowe. Na każdej osi liczbowej kropkami zaznaczono dwie liczby i liczbę  .
.
Na którym rysunku liczba  jest sumą dwóch pozostałych liczb?
jest sumą dwóch pozostałych liczb?
Zaznacz dobrą odpowiedź.
Zaznacz zdanie fałszywe.
A) Jeżeli liczba jest podzielna przez 12, to jest podzielna przez 6.
B) Jeżeli liczba jest podzielna przez 6, to jest podzielna przez 3 i przez 2.
C) Jeżeli liczba jest podzielna przez 3 i przez 5, to jest podzielna przez 15.
D) Jeżeli liczba jest podzielna przez 3 i przez 6, to jest podzielna przez 18.
Do pojemnika wsypano 200 koralików białych i 300 czerwonych. Wymieszano je i zapakowano do woreczków po 50 sztuk. Okazało się, że w jednym z woreczków znalazły się tylko białe koraliki.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Wobec tego nie jest możliwe, aby
A) wszystkie pozostałe białe koraliki znajdowały się w trzech woreczkach.
B) w jednym z pozostałych woreczków nie było białych koralików.
C) w większości pozostałych woreczków znalazło się po 17 białych koralików.
D) w każdym z pozostałych woreczków było więcej koralików białych niż czerwonych.
W szufladzie znajduje się 10 par skarpetek, w tym 3 pary skarpetek czarnych. Tomek losowo wyjmuje po jednej skarpetce z szuflady.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F jeśli jest fałszywe.
| Tomek, aby mieć pewność, że przynajmniej dwie wyjęte skarpetki będą czarne, musi wyjąć co najmniej 16 skarpetek. | P | F |
| Tomek za pierwszym razem nie wyjął czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wyjmie czarną skarpetkę, wzrosło. | P | F |
Pan Jerzy wyjechał z pewnego miasta samochodem w trasę liczącą 210 km o godzinie 9:30. Dziesięć minut później z tego samego miasta wyjechał w tę samą trasę pan Wojciech. Wykresy przedstawiają zależność drogi przebytej przez obu kierowców od czasu jazdy.
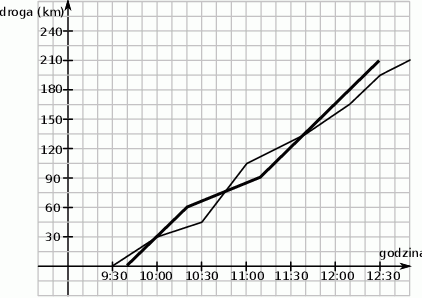
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| O godzinie 10:30 bliżej celu był pan Wojciech. | P | F |
| Większą średnią prędkość na całej trasie uzyskał samochód pana Jerzego. | P | F |
Dana jest funkcja określona wzorem 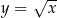 , gdzie
, gdzie  jest liczbą dodatnią.
jest liczbą dodatnią.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wartości tej funkcji są zawsze dodatnie. | P | F |
Punkt 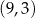 należy do wykresu tej funkcji. należy do wykresu tej funkcji. | P | F |
Dany jest układ równań
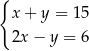
Dokończ zdanie. Zaznacz dobrą odpowiedź.
Liczby  i
i 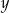 spełniające ten układ równań spełniają też warunek:
spełniające ten układ równań spełniają też warunek:
A)  i
i 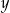 są liczbami parzystymi. B)
są liczbami parzystymi. B)  i
i 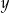 są liczbami ujemnymi.
są liczbami ujemnymi.
C) suma  i
i 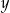 jest podzielna przez 3. D) różnica
jest podzielna przez 3. D) różnica  i
i 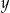 jest równa 0.
jest równa 0.
W dwóch zbiornikach znajduje się 420 litrów mleka. Jeśli z pierwszego zbiornika przelejemy do drugiego  jego zawartości, to w obu zbiornikach będzie taka sama ilość mleka.
jego zawartości, to w obu zbiornikach będzie taka sama ilość mleka.
Ile litrów mleka jest w pierwszym zbiorniku? Wybierz odpowiedź spośród podanych.
A) 175 B) 229 C) 245 D) 252
Do pięciu różnych naczyń rozlano 6 litrów wody.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Średnia arytmetyczna ilości wody w tych naczyniach zmieni się, gdy
A) jedno naczynie opróżnimy, przelewając jego zawartość do pozostałych naczyń.
B) poprzelewamy wodę z jednego naczynia do drugiego, tak by w każdym naczyniu było jej tyle samo.
C) z czterech naczyń odlejemy trochę wody do piątego naczynia.
D) do każdego naczynia dolejemy taką samą ilość wody.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Długość przekątnej prostokąta przedstawionego na rysunku jest równa
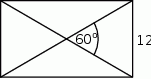
A) 12 B) 16 C) 20 D) 24
Przedstawiony na rysunku trójkąt 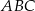 jest prostokątny, ale nie jest równoramienny. Odcinek
jest prostokątny, ale nie jest równoramienny. Odcinek 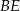 jest wysokością w trójkącie
jest wysokością w trójkącie 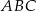 , a półprosta
, a półprosta 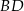 jest dwusieczną kąta prostego.
jest dwusieczną kąta prostego.
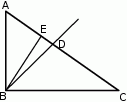
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
Półprosta 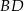 jest dwusieczną kąta jest dwusieczną kąta 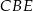 . . | P | F |
Odcinek 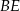 jest wysokością w trójkącie jest wysokością w trójkącie 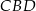 . . | P | F |
Dokończ zdanie. Zaznacz dobrą odpowiedź.
Na planie pokoju w skali 1 : 50 prostokątna podłoga ma wymiary 8 cm i 12 cm. W skali 1 : 1 pole powierzchni podłogi tego pokoju jest równe
A) 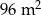 B)
B) 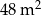 C)
C) 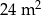 D)
D) 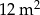
Wykonano następującą konstrukcję.
1. Narysowano trójkąt 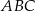 . 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą
. 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą 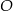 .
.
3. Poprowadzono prostą prostopadłą do boku 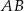 i przechodzącą przez punkt
i przechodzącą przez punkt 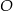 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 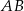 oznaczono literą
oznaczono literą 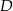 .
.
4. Narysowano okrąg o środku w punkcie 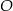 i promieniu
i promieniu 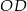 .
.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trójkąta.
B) jest styczny do wszystkich boków tego trójkąta.
C) ma środek leżący na jednym z boków trójkąta.
D) przecina jeden z boków trójkąta w dwóch punktach.
Bryłę ułożono z jednakowych sześciennych klocków. Na rysunkach przedstawiony jest widok tej bryły z dwóch stron.
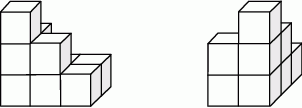
Z ilu klocków składa się ta bryła? Zaznacz dobrą odpowiedź.
A) 7 B) 8 C) 9 D) 10
Czy kulę o objętości 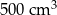 można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | średnica kuli jest mniejsza od przekątnej kwadratu. |
| B) | średnica kuli jest mniejsza od boku kwadratu. |
| C) | średnica kuli jest większa od przekątnej kwadratu. |
| D) | średnica kuli jest większa od boku kwadratu. |
Do czterech naczyń 1, 2, 3 i 4 (patrz rysunek) o tej samej pojemności równej 300 ml wlano po 150 ml wody. W dwóch naczyniach wodę wlano dokładnie do połowy ich wysokości.

Które to naczynia? Zaznacz dobrą odpowiedź.
A) 1 i 2 B) 1 i 3 C) 2 i 4 D) 3 i 4
Na wycieczkę wyjechało 38 uczniów. Dzieci spały w 15 pokojach. Dziewczynki spały w pokojach dwuosobowych, a chłopcy spali w pokojach trzyosobowych. Wszystkie miejsca w pokojach były zajęte. Ile dziewczynek i ilu chłopców było na wycieczce? Zapisz obliczenia.
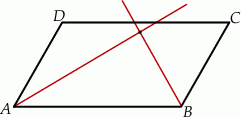
Uzasadnij, że dwusieczne kątów 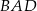 i
i 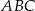 równoległoboku
równoległoboku  są prostopadłe.
są prostopadłe.
Na rysunkach przedstawiono tę samą bryłę widzianą z dwóch stron. Każda ze ścian tej bryły jest albo kwadratem, albo trójkątem równobocznym. Kwadratem jest też czworokąt  (patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
(patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.