/Gimnazjum/Egzamin gimnazjalny/Egzamin 2012
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 31 marca 2012 Czas pracy: 90 minut
Kierowca samochodu dostawczego zanotował w tabeli informacje o 6 wyjazdach służbowych.
| L. p. | Liczba przejechanych kilometrów | Czas podróży |
| 1. | 170 | 2 h 50 min |
| 2. | 160 | 2 h 20 min |
| 3. | 120 | 2 h |
| 4. | 150 | 2 h 20 min |
| 5. | 310 | 5 h 10 min |
| 6. | 190 | 3 h 10 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie prawdziwe.
A) Kierowca w ciągu jednego wyjazdu przejeżdżał średnio 180 km.
B) Trzy pierwsze wyjazdy trwały dłużej, niż trzy kolejne.
C) Podczas dwóch pierwszych wyjazdów kierowca przejechał 30% łącznej liczby kilometrów przejechanych podczas 6 wyjazdów.
D) Średnia prędkość podczas każdego z wyjazdów wyniosła 60 km/h.
Grupa uczniów jechała pociągiem w góry. Jedna siódma uczniów miała miejsca przy oknie, jedna piąta uczniów miała miejsca przy korytarzu, a pozostali uczniowie mieli miejsca środkowe.
Jaki procent wszystkich uczniów stanowią uczniowie, którzy nie mieli miejsc przy korytarzu? Zaznacz dobrą odpowiedź.
A) 75% B) 60% C) 20% D) 80%
Pewna agencja reklamowa przygotowała zestawy promocyjne, które zawierały długopisy, ołówki i notesy. W każdym zestawie była taka sama liczba długopisów, ołówków i notesów, a łącznie we wszystkich zestawach znalazło się 225 długopisów, 300 ołówków i 150 notesów.
Ile maksymalnie przygotowano zestawów reklamowych? Wybierz odpowiedź spośród podanych.
A) 90 B) 75 C) 50 D) 25
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Liczbę 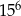 można zapisać jako
można zapisać jako
A) 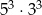 B)
B) 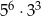 C)
C) 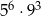 D)
D) 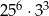
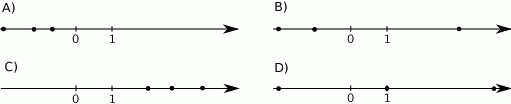
Na rysunkach przedstawiono osie liczbowe. Na każdej osi liczbowej kropkami zaznaczono trzy liczby  .
.
Na którym rysunku zaznaczone liczby spełniają warunek  ?
?
Zaznacz dobrą odpowiedź.
Adam i Wojtek mają razem 82 cukierki. Jeżeli każdy z chłopców zje 29 cukierków, to Adam będzie miał trzy razy mniej cukierków niż Wojtek.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli Wojtek odda Adamowi 6 cukierków, to chłopcy będą mieli taką samą liczbę cukierków. | P | F |
| Jeżeli każdy z chłopców zje 23 cukierki, to Wojtek będzie miał dwa razy więcej cukierków niż Adam. | P | F |
Zaznacz zdanie fałszywe.
A) Każdy równoległobok posiada środek symetrii.
B) Każdy równoległobok posiada oś symetrii.
C) Każdy romb posiada środek symetrii.
D) Każdy romb posiada oś symetrii.
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
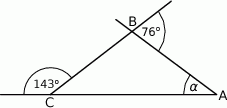
A) 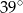 B)
B) 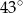 C)
C) 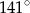 D)
D) 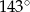
Informacja do zadań 9 i 10
Pan Antoni wyjechał o godzinie 9:00 w podróż samochodową z Torunia do Warszawy. W tym samym czasie pan Kamil wyruszył w drogę w odwrotnym kierunku, z Warszawy do Torunia. Wykresy przedstawiają odległość każdego z kierowców od Torunia w zależności od czasu jazdy.
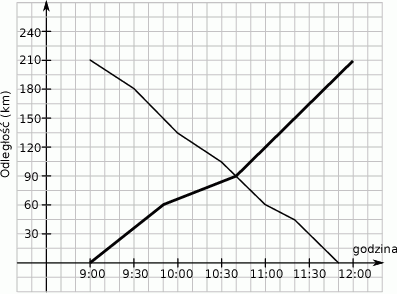
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| O godzinie 10:30 pan Antoni był bliżej Warszawy niż pan Kamil. | P | F |
| Samochody minęły się w trakcie podróży bliżej Torunia niż Warszawy. | P | F |
Z jaką największą prędkością poruszał się pan Antoni? Wybierz odpowiedź spośród podanych
A) 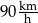 B)
B) 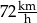 C)
C) 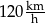 D)
D) 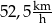
Na którym rysunku łuk narysowany linią ciągłą jest 4 razy krótszy od łuku narysowanego linią przerywaną?
Zaznacz poprawną odpowiedź.
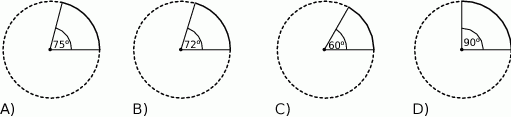
Do pięciu różnych pojemników włożono kulki w dwóch kolorach. W sumie włożono 36 kulek niebieskich i 48 kulek czerwonych.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Stosunek liczby kulek niebieskich do liczby kulek czerwonych zawartych we wszystkich pojemnikach nie zmieni się gdy
A) do każdego pojemnika dołożymy 12 kulek czerwonych i 12 kulek niebieskich.
B) w każdym pojemniku zwiększymy trzykrotnie liczbę kulek niebieskich i czterokrotnie liczbę kulek czerwonych.
C) do każdego pojemnika dołożymy 15 kulek niebieskich i 20 kulek czerwonych.
D) do każdego pojemnika dołożymy 12 kulek czerwonych i 24 kulki niebieskie.
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Równość 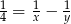 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce  i
i 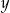 zostaną wpisane liczby
zostaną wpisane liczby
A) 3 i 15 B) 6 i 12 C) 3 i 6 D) 3 i 12
Wykonano następującą konstrukcję.
1. Narysowano romb 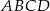 .
.
2. Wykreślono przekątne rombu i ich punkt przecięcia oznaczono literą 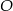 .
.
3. Poprowadzono prostą prostopadłą do boku 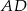 i przechodzącą przez punkt
i przechodzącą przez punkt 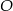 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 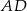 oznaczono literą
oznaczono literą 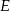 .
.
4. Narysowano okrąg o środku w punkcie 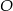 i promieniu
i promieniu 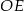 .
.
Dokończ poniższe zdanie, wybierając odpowiedź spośród podanych.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego rombu.
B) jest styczny do wszystkich boków tego rombu.
C) jest styczny do przekątnych tego rombu.
D) nie ma punktów wspólnych z jednym z boków rombu.
Uczniowie na zimowisku zostali podzielni na 4 grupy. Tabela zawiera informację o liczbie uczniów w poszczególnych grupach z podziałem ze względu na ich wiek.
| Wiek | Grupa I | Grupa II | Grupa III | Grupa IV |
| 10 lat | 20 | 10 | 30 | 20 |
| 11 lat | 30 | 10 | 20 | 0 |
| 12 lat | 40 | 30 | 30 | 20 |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Prawdopodobieństwo, że losowo wybrany uczeń grupy ma 12 lat jest największe, gdy ucznia losujemy z grupy
A) I B) II C) III D) IV
Dokończ zdanie. Zaznacz dobrą odpowiedź.
Na planie budowlanym w skali 1 : 75 działka budowlana jest kwadratem o przekątnej długości 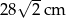 . W rzeczywistości pole tej działki jest równe
. W rzeczywistości pole tej działki jest równe
A) 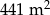 B)
B) 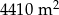 C)
C) 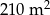 D)
D) 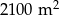
Zaznacz zdanie fałszywe.
A) Liczba krawędzi każdego ostrosłupa jest liczbą parzystą.
B) Liczba krawędzi każdego graniastosłupa dzieli się przez 3.
C) Liczba krawędzi każdego ostrosłupa dzieli się przez 3.
D) Liczba wierzchołków każdego graniastosłupa jest liczbą parzystą.
Brzeg narysowanej figury składa się 5 półokręgów.
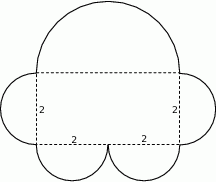
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Pole tej figury jest równe
A) 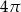 B)
B) 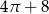 C)
C) 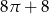 D)
D) 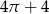
Dokończ zdanie. Wybierz odpowiedź spośród podanych. Przedstawiona na wykresie funkcja przyjmuje wartości ujemne jeżeli
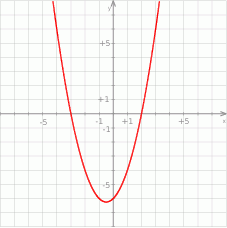
A) 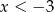 B)
B) 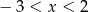 C)
C) 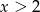 D)
D) 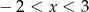
Naczynie w kształcie walca napełniamy nalewając do niego wodę naczyniem w kształcie stożka o takiej samej wysokości i promieniu podstawy.
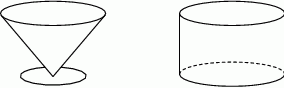
Ile razy należy należy przelać wodę z naczynia w kształcie stożka (całkowicie napełnionego) do naczynia w kształcie walca, aby je całkowicie napełnić? Zaznacz dobrą odpowiedź.
A) 2 razy B) 3 razy C) 4 razy D) 9 razy
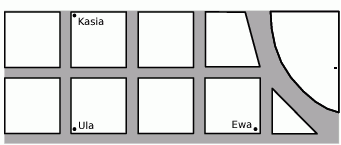
Na schematycznym planie miasta zaznaczono położenie domów trzech koleżanek: Kasi, Uli i Ewy. Odległość między domami Kasi i Uli jest równa 900 m, a odległość między domami Uli i Ewy jest równa 1,2 km. Oblicz odległość (mierzoną w linii prostej) między domami Kasi i Ewy. Zapisz obliczenia.
Kasia napisała na tablicy 6 kolejnych wielokrotności liczby 9. Uzasadnij, że suma pierwszych trzech z tych liczb jest o 81 mniejsza od sumy trzech ostatnich.
Z 36 identycznych plastikowych sześcianów o krawędzi długości 1 cm zbudowano graniastosłup prawidłowy czworokątny. Jakie jest największe możliwe pole powierzchni tego graniastosłupa? Zapisz obliczenia.

