/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 16 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Wyrażenie 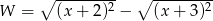 dla
dla 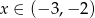 przyjmuje postać
przyjmuje postać
A) 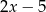 B)
B) 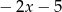 C) -1 D)
C) -1 D) 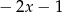
Spodnie po serii obniżek ceny o 10% kosztują 393,66 zł. Oblicz ile razy obniżono cenę spodni o 10% jeżeli cena spodni po drugiej obniżce wynosiła 540 zł.
A) 3 B) 4 C) 5 D) 6
O liczbie dodatniej 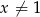 wiadomo, że
wiadomo, że 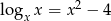 . Zatem
. Zatem
A) 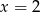 B)
B) 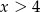 C)
C) 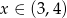 D)
D) 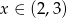
Liczba 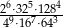 jest równa
jest równa
A) 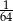 B) 32 C) 64 D)
B) 32 C) 64 D) 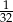
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
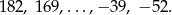
Ile liczb napisano na tablicy?
A) 17 B) 18 C) 19 D) 20
Wartość wyrażenia 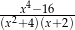 dla
dla 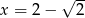 jest równa
jest równa
A) 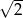 B)
B) 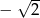 C) 2 D) -2
C) 2 D) -2
Rozwiązaniem nierówności 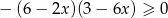 jest zbiór
jest zbiór
A) 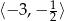 B)
B) 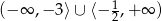 C)
C) 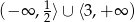 D)
D) 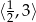
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 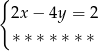 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 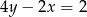 B)
B) 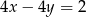 C)
C) 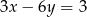 D)
D) 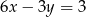
Prosta o równaniu 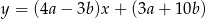 przecina oś
przecina oś 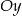 w punkcie
w punkcie 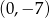 . Wtedy
. Wtedy
A) 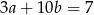 B)
B) 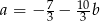 C)
C) 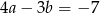 D)
D) 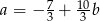
Na rysunku przedstawiony jest wykres funkcji 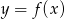 .
.
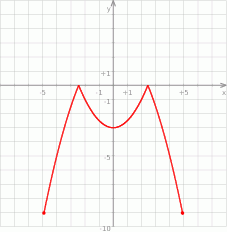
Które z równań ma dokładnie trzy rozwiązania?
A) 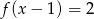 B)
B) 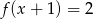 C)
C) 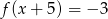 D)
D) 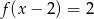
Osią symetrii paraboli będącej wykresem funkcji 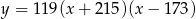 jest prosta o równaniu
jest prosta o równaniu
A) 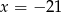 B)
B) 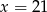 C)
C) 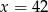 D)
D) 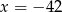
Na podstawie fragmentu wykresu funkcji kwadratowej 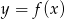 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
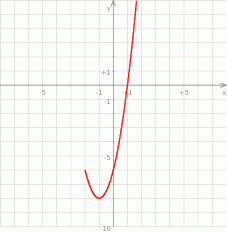
A) Jeżeli 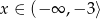 to
to 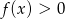 .
.
B) Do wykresu funkcji należy punkt 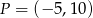 .
.
C) Wartości funkcji są dodatnie dla 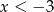 .
.
D) Miejscami zerowymi funkcji 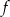 są liczby: 1 oraz -4.
są liczby: 1 oraz -4.
Do wykresu funkcji 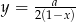 dla
dla 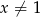 należy punkt
należy punkt 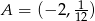 . Wtedy
. Wtedy
A) 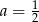 B)
B) 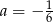 C)
C) 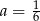 D)
D) 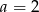
W ciągu geometrycznym 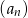 dane są
dane są 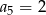 i
i 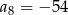 . Wtedy
. Wtedy
A) 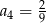 B)
B) 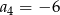 C)
C) 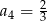 D)
D) 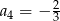
Kąt  jest ostry i
jest ostry i 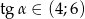 . Wtedy liczba
. Wtedy liczba 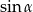 należy do przedziału
należy do przedziału
A) 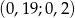 B)
B) 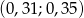 C)
C) 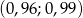 D)
D) 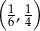
Dane są dwie proste równoległe 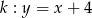 oraz
oraz 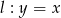 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 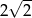 C)
C) 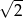 D) 4
D) 4
Pole trójkąta równobocznego wpisanego w koło o polu 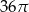 jest równe
jest równe
A) 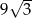 B) 81 C)
B) 81 C) 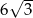 D)
D) 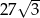
Wykresy funkcji 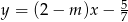 i
i 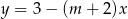 są prostopadłe. Zatem
są prostopadłe. Zatem 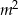
A) jest liczbą parzystą
B) jest liczbą wymierną
C) jest równe 0
D) jest liczbą niewymierną
Długość odcinka 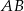 o końcach
o końcach 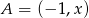 i
i 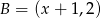 jest równa 6. Wtedy
jest równa 6. Wtedy
A) 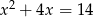 B)
B) 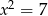 C)
C) 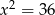 D)
D)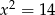
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 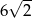 , a krawędź boczna ma długość 10. Wysokość ostrosłupa ma długość
, a krawędź boczna ma długość 10. Wysokość ostrosłupa ma długość
A) 6 B) 8 C) 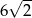 D)
D) 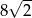
Wskaż równanie paraboli, której osią symetrii jest prosta 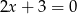 .
.
A) 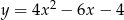
B) 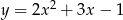
C) 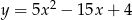
D) 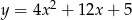
W trapezie prostokątnym podstawy mają długości 6 i 9. Która z liczb nie może być długością dłuższego ramienia trapezu?
A) 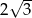 B)
B) 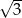 C)
C) 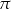 D)
D) 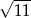
Iloczyn długości wszystkich krawędzi sześcianu jest równy 16. Objętość tego sześcianu jest równa
A) 12 B) 2 C) 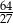 D)
D) 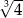
Ile można utworzyć liczb czterocyfrowych podzielnych przez 20, o cyfrach należących do zbioru 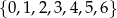 ?
?
A) 168 B) 196 C) 144 D) 126
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Zadania otwarte
Uzasadnij, że jeśli 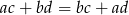 to
to 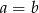 lub
lub 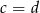 .
.
Rozwiąż równanie 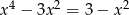 .
.
Punkty 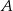 i
i 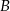 są punktami wspólnymi dwóch okręgów, a odcinki
są punktami wspólnymi dwóch okręgów, a odcinki 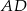 i
i 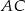 ich średnicami.
ich średnicami.
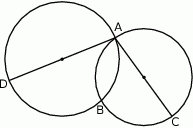
Wykaż, że punkt 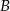 leży na prostej przechodzącej przez punkty
leży na prostej przechodzącej przez punkty 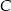 i
i 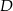 .
.
W prostokącie 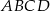 połączono wierzchołki
połączono wierzchołki 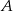 i
i 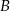 ze środkiem boku
ze środkiem boku 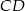 i otrzymano trójkąt, którego jeden z kątów ma miarę
i otrzymano trójkąt, którego jeden z kątów ma miarę 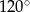 . Wiedząc, że
. Wiedząc, że 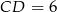 oblicz obwód prostokąta
oblicz obwód prostokąta 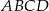 .
.
Wykaż, że rozwiązaniem nierówności 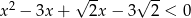 jest przedział
jest przedział 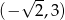 .
.
Objętość prostopadłościanu jest równa 2400, a mniejsza z jego ścian bocznych ma pole powierzchni 120. Gdyby krótszą z jego krawędzi podstawy wydłużyć o 2, a dłuższą wydłużyć o 5 to objętość prostopadłościanu wzrosłaby o 1100. Oblicz wymiary prostopadłościanu.
W trójkącie 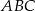 , gdzie
, gdzie 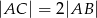 dane są
dane są 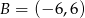 i
i 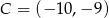 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 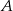 , jeżeli leży on na prostej
, jeżeli leży on na prostej 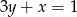 .
.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 40, a pole 60.

