/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 2 kwietnia 2011 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Określ liczbę pierwiastków równania 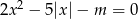2 2x − 5|x|− m = 0 w zależności od wartości parametru m .

Zadanie 2
(4 pkt)

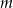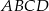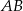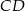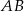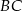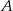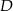Dany jest trapez prostokątny ABCD o podstawach AB i CD , w którym boki AB i BC są prostopadłe. Dwusieczne kątów A i D przecinają się w punkcie 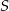S leżącym na boku 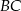BC . Wykaż, że |BS | = |SC | .

Zadanie 3
(5 pkt)

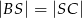Wielomian 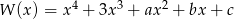W (x) = x4 + 3x3 + ax2 + bx + c jest podzielny przez trójmian 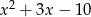x2 + 3x − 10 , a przy dzieleniu przez dwumian 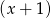(x + 1) daje resztę -36. Wyznacz współczynniki 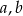a,b i c wielomianu.

Zadanie 4
(5 pkt)

Podstawy czterech logarytmów liczby x tworzą ciąg geometryczny o ilorazie x . Wyznacz pierwszy z tych logarytmów jeśli jest on mniejszy od -1 oraz suma dwóch pierwszych logarytmów jest równa sumie dwóch pozostałych

Zadanie 5
(5 pkt)

Wyznacz zbiór wartości funkcji: 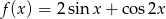f (x) = 2 sin x + cos 2x , gdzie x ∈ R .

Zadanie 6
(5 pkt)

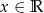Punkt 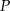P jest punktem wspólnym przekątnych trapezu 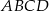ABCD , w którym 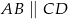AB ∥ CD oraz −→ −→ −→ D = (1 0,− 9),AB = [12,21],CB = [0,13],CP = [− 3,− 2] . Oblicz współrzędne pozostałych wierzchołków trapezu ABCD .

Zadanie 7
(4 pkt)

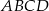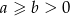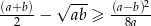Udowodnij, że jeżeli a ≥ b > 0 to √ --- 2 (a+2b) − ab ≥ (a−8ba)-- .

Zadanie 8
(4 pkt)

W trójkącie prostokątnym 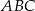ABC cosinus i tangens kąta przy wierzchołku 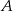A są równe. Oblicz sinus tego kąta.

Zadanie 9
(5 pkt)

Wyznacz współrzędne punktu 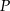P leżącego na wykresie funkcji 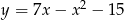y = 7x − x2 − 15 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza.

Zadanie 10
(4 pkt)

Trójkąt prostokątny o przyprostokątnych długości 12 i 7 obraca się wokół przeciwprostokątnej. Oblicz promień kuli wpisanej w otrzymaną bryłę.

Zadanie 11
(5 pkt)

Ze zbioru wszystkich liczb trzycyfrowych, które są podzielne przez 7 wybieramy losowo 5 różnych liczb. Oblicz prawdopodobieństwo tego, że jedną z tych liczb jest 546, a wśród pozostałych 4 liczb jest dokładnie jedna liczba mniejsza od 546. Wynik podaj w postaci ułamka nieskracalnego.

Arkusz Wersja PDF
Rozwiązania