/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 16 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczbę 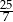 zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
A) 0,008% B) 8% C) 0,8% D) 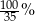
Liczba 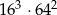 jest równa
jest równa
A) 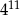 B)
B) 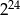 C)
C) 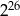 D)
D) 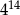
Wartość wyrażenia 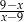 dla
dla 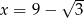 jest równa
jest równa
A) 1 B) 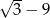 C)
C) 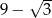 D) -1
D) -1
Jeżeli 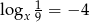 to liczba
to liczba  jest równa
jest równa
A) 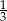 B) 3 C)
B) 3 C) 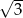 D)
D) 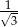
Dany jest ciąg 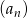 o wyrazie ogólnym
o wyrazie ogólnym 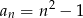 , gdzie
, gdzie 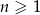 . Wówczas
. Wówczas
A) 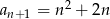 B)
B) 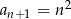 C)
C) 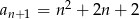 D)
D) 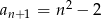
Rozwiązaniem równania 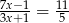 jest
jest
A) 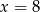 B)
B) 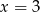 C)
C) 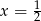 D)
D) 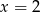
Liczba pierwiastków rzeczywistych wielomianu 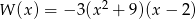 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Mniejszą z dwóch liczb spełniających równanie 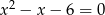 jest
jest
A) -6 B) -3 C) -2 D) -1
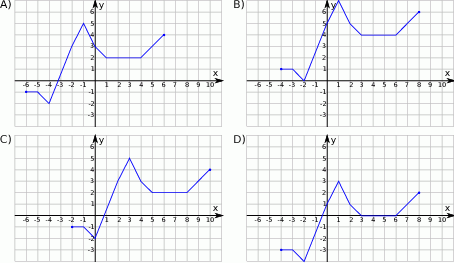
Rysunek przedstawia wykres funkcji 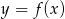 .
.
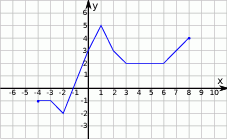
Wskaż wykres funkcji 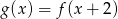 .
.
Wartość wyrażenia 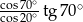 wynosi
wynosi
A) 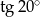 B)
B) 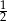 C) 1 D)
C) 1 D) 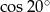
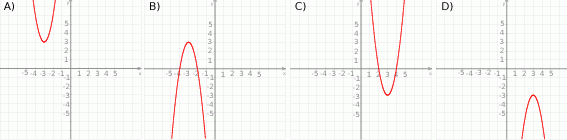
Zbiorem wartości funkcji kwadratowej 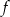 jest przedział
jest przedział 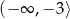 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 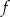 ?
?
Wskaż 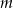 , dla którego funkcja liniowa określona wzorem
, dla którego funkcja liniowa określona wzorem 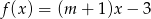 jest stała.
jest stała.
A) 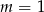 B)
B) 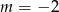 C)
C) 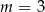 D)
D) 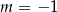
W ciągu geometrycznym 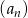 dane są:
dane są: 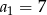 i
i 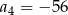 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 2 B) 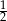 C)
C) 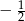 D) -2
D) -2
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 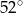 jest równa
jest równa
A) 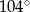 B)
B) 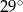 C)
C) 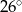 D)
D) 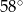
W ciągu arytmetycznym 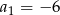 oraz
oraz 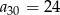 . Wtedy suma
. Wtedy suma 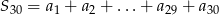 jest równa
jest równa
A) 240 B) 4680 C) 270 D) 540
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 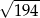 B)
B) 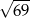 C) 12 D) 11
C) 12 D) 11
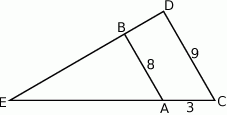
Oblicz długość odcinka 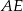 wiedząc, że
wiedząc, że 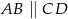 i
i 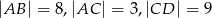 .
.
A) 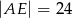 B)
B) 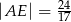 C)
C) 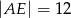 D)
D) 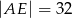
Objętość walca o promieniu podstawy  i wysokości 2 razy mniejszej od promienia jest równa
i wysokości 2 razy mniejszej od promienia jest równa
A) 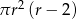 B)
B) 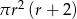 C)
C) 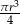 D)
D) 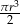
Promień okręgu o równaniu 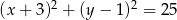 jest równy
jest równy
A) 25 B) 5 C) 625 D) 15
Graniastosłup ma 18 krawędzi. Ile wierzchołków ma ten graniastosłup?
A) 18 B) 6 C) 12 D) 24
Wszystkich liczb dwucyfrowych o różnych cyfrach jest
A) 90 B) 81 C) 82 D) 80
Zadania otwarte
Rozwiąż nierówność: 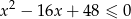 .
.
Rozwiąż równanie 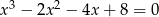 .
.
W układzie współrzędnych na płaszczyźnie punkty 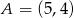 i
i 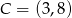 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 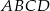 . Wyznacz równanie prostej
. Wyznacz równanie prostej 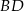 .
.
W trójkącie równobocznym 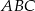 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 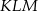 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 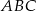 i
i 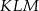 .
.
Uzasadnij, że jeśli 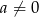 oraz
oraz 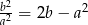 , to
, to 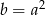 .
.
Kąt  jest ostry oraz
jest ostry oraz 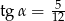 . Oblicz
. Oblicz 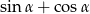 .
.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 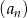 wyraża się wzorem
wyraża się wzorem 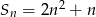 dla
dla 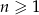 . Oblicz pierwszy wyraz ciągu i jego różnice.
. Oblicz pierwszy wyraz ciągu i jego różnice.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 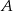 polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 6.
polegającego na tym, że w pierwszym rzucie otrzymamy nieparzystą liczbę oczek i iloczyn liczb oczek w obu rzutach będzie podzielny przez 6.
Krótsza podstawa trapezu ma długość 2, a ramiona długości 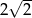 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 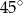 i
i 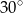 . Oblicz pole trapezu.
. Oblicz pole trapezu.
Dwa motocykle wyjechały z miast 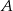 i
i 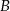 oddalonych od siebie o 360 km. Motocykl jadący z miasta
oddalonych od siebie o 360 km. Motocykl jadący z miasta 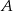 do miasta
do miasta 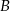 wyjechał o 30 minut wcześniej niż motocykl jadący z miasta
wyjechał o 30 minut wcześniej niż motocykl jadący z miasta 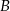 do miasta
do miasta 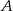 i jechał z prędkością o 12 km/h mniejszą. Motocykle te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te motocykle.
i jechał z prędkością o 12 km/h mniejszą. Motocykle te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te motocykle.

