/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom podstawowy 13 stycznia 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczba 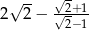 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) większą niż 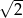 D) naturalną
D) naturalną
Liczba 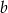 to 125% liczby
to 125% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 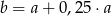 B)
B) 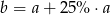 C)
C) 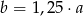 D)
D) 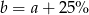
Liczby należące do przedziału 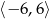 są rozwiązaniami nierówności
są rozwiązaniami nierówności
A) 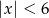 B)
B) 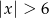 C)
C) 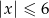 D)
D) 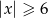
Jeżeli 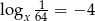 to liczba
to liczba  jest równa
jest równa
A) 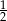 B)
B) 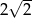 C) 2 D) 4
C) 2 D) 4
Połowa liczby 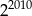 to
to
A) 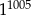 B)
B) 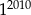 C)
C) 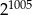 D)
D) 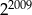
Iloczyn wielomianów 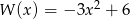 i
i 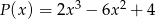 jest wielomianem stopnia
jest wielomianem stopnia
A) 2 B) 3 C) 5 D) 6
Liczba ![[ ] log4 lo g3(log28 )](https://img.zadania.info/zes/0055478/HzesT24x.gif) jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Wartość wyrażenia 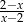 dla
dla 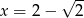 jest równa
jest równa
A) -1 B) 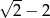 C)
C) 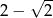 D) 1
D) 1
Najmniejszą liczbą naturalną, która nie spełnia nierówności 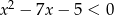 jest
jest
A) 0 B) 3 C) 7 D) 8
Na rysunku przedstawiony jest wykres funkcji liniowej 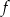 .
.
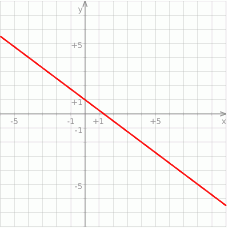
Funkcja 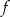 jest określona wzorem
jest określona wzorem
A) 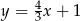 B)
B) 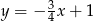 C)
C) 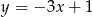 D)
D) 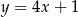
Osią symetrii wykresu funkcji 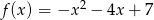 jest prosta o równaniu
jest prosta o równaniu
A) 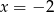 B)
B) 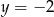 C)
C) 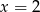 D)
D) 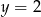
Wartość wyrażenia 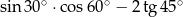 jest równa
jest równa
A) 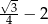 B)
B) 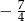 C)
C) 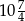 D)
D) 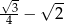
Rozwiązaniem równania 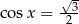 dla
dla 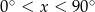 jest
jest
A) 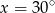 B)
B) 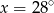 C)
C) 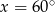 D)
D) 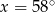
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 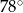 jest równa
jest równa
A) 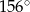 B)
B) 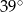 C)
C) 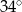 D)
D) 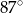
Maksymalny przedział, w którym funkcja 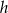 (rysunek poniżej)
(rysunek poniżej)
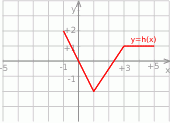
jest rosnąca to
A) 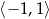 B)
B) 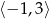 C)
C) 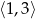 D)
D) 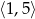
W trapezie prostokątnym kąt ostry ma miarę 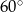 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 6 B) 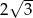 C)
C) 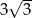 D)
D) 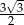
Długość odcinka  jest równa
jest równa
A) 6 B) 3 C) 2 D) 4
Suma długości wszystkich krawędzi sześcianu jest równa 24. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 24 D) 64
Objętość kuli o promieniu 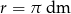 jest równa
jest równa
A) 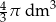 B)
B) 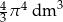 C)
C) 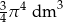 D)
D) 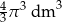
Prawdopodobieństwo zdarzenia 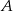 jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 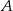 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 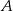 jest równe
jest równe
A)  B)
B) 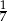 C)
C)  D)
D) 
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których pierwsza cyfra jest parzysta, a druga nieparzysta?
A) 16 B) 20 C) 24 D) 25
Liczba dodatnich wyrazów ciągu 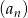 określonego wzorem
określonego wzorem 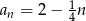 , gdzie
, gdzie 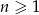 jest równa
jest równa
A) 8 B) 4 C) 16 D) 7
Zadania otwarte
Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w drugim rzucie wypadnie parzysta liczba oczek.
Rozwiąż nierówność 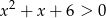 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 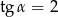 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 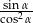 .
.
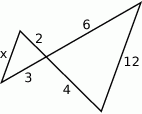
Punkty 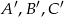 są środkami boków trójkąta
są środkami boków trójkąta 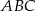 . Pole trójkąta
. Pole trójkąta 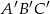 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta 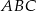 .
.
Wykaż, że różnica kwadratów dwóch kolejnych liczb parzystych jest liczbą podzielną przez 4.
Proste o równaniach 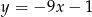 i
i 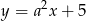 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Prosta przechodząca przez wierzchołek 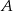 równoległoboku
równoległoboku 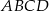 przecina jego przekątną
przecina jego przekątną 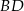 w punkcie
w punkcie 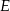 i bok
i bok 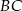 w punkcie
w punkcie 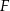 , a prostą
, a prostą 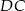 w punkcie
w punkcie 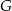 . Udowodnij, że
. Udowodnij, że
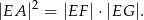
W trapezie równoramiennym 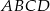 ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie 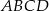 jest równy
jest równy  , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
Trzy liczby ciąg arytmetyczny. Ich suma jest równa 15. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o jeden to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.
Oblicz pole czworokąta 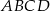 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 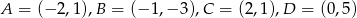 .
.

