/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas trzecich)
poziom rozszerzony 12 stycznia 2011 Czas pracy: 180 minut
Wyznacz dziedzinę funkcji określonej wzorem 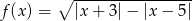 .
.
Nieskończony ciąg liczbowy 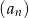 określony jest wzorem:
określony jest wzorem:
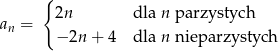
- Wyznacz sumę dwudziestu początkowych wyrazów ciągu.
- Zbadaj, czy istnieje wyraz ciągu równy 5. Odpowiedź uzasadnij.
W kąt o mierze 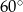 wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.
wpisano pięć kół tak, że każde następne koło poza pierwszym, jest styczne zewnętrznie do koła poprzedniego. Oblicz ile razy suma pól wszystkich kół jest większa od pola najmniejszego koła.
Naszkicuj wykres funkcji 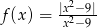 . Określ dziedzinę oraz zbiór wartości funkcji.
. Określ dziedzinę oraz zbiór wartości funkcji.
Wyznacz zbiór wartości parametru 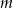 , dla których równanie:
, dla których równanie: 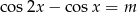 ma rozwiązania.
ma rozwiązania.
Prosta 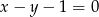 jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty
jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty 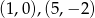 są jego wierzchołkami. Znajdź pozostałe wierzchołki.
są jego wierzchołkami. Znajdź pozostałe wierzchołki.
Trapez równoramienny o obwodzie 20 dm i przekątnej długości 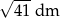 jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.
jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.
Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 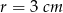 . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
. Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
Udowodnij, że 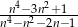 , dla
, dla 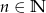 i
i 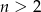 jest ułamkiem właściwym.
jest ułamkiem właściwym.
Ile maksymalnie kul zielonych można włożyć do urny, w której jest 7 kul czerwonych, aby prawdopodobieństwo wylosowania 2 kul różnokolorowych było większe lub równe 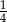 ?
?
W trapezie 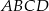 połączono środek
połączono środek 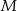 ramienia trapezu
ramienia trapezu 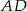 z końcami drugiego ramienia
z końcami drugiego ramienia 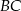 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 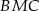 jest równe połowie pola trapezu
jest równe połowie pola trapezu 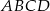 .
.

