Zadanie nr 5376510
Z wierzchołków sześcianu  losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu  , jest równe
, jest równe
A) 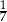 B)
B) 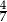 C)
C) 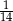 D)
D) 
Rozwiązanie
Sposób I
Dwa różne wierzchołki sześcianu możemy wybrać na
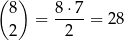
sposobów. Jednocześnie są cztery zdarzenia sprzyjające – bo tyle przekątnych ma sześcian.
Interesujące nas prawdopodobieństwo jest więc równe
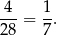
Sposób II
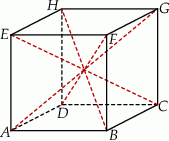
Dwa różne wierzchołki sześcianu zawsze są końcami jego krawędzi, przekątnej ściany bocznej lub też przekątnej sześcianu. W sumie jest
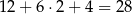
takich odcinków. Wśród nich są 4 przekątne sześcianu, więc interesujące nas prawdopodobieństwo jest równe
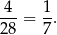
Sposób III
O zdarzeniach elementarnych myślimy jak o parach 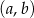 , gdzie
, gdzie  i
i 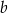 są różnymi wierzchołkami sześcianu. Jest więc
są różnymi wierzchołkami sześcianu. Jest więc
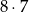
zdarzeń elementarnych. Wśród nich jest 8:
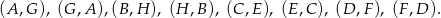
zdarzeń sprzyjających. Interesujące nas prawdopodobieństwo jest więc równe
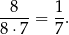
Odpowiedź: A

