Zadanie nr 8348239
Losujemy jeden wierzchołek i jedną ścianę sześcianu. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe
A) 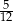 B)
B) 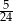 C)
C) 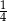 D)
D) 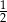
Rozwiązanie
O zdarzeniach elementarnych myślimy jak o parach 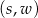 , gdzie
, gdzie  jest ścianą, a
jest ścianą, a 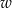 wierzchołkiem. Wszystkich zdarzeń elementarnych jest
wierzchołkiem. Wszystkich zdarzeń elementarnych jest
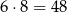
(bo sześcian ma 6 ścian i 8 wierzchołków).
Obliczmy ile jest zdarzeń sprzyjających: dla każdej ściany są cztery odpowiednie wierzchołki, więc razem jest
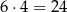
sprzyjających par. Zatem prawdopodobieństwo wynosi
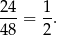
Odpowiedź: D

