Zadanie nr 1604228
W graniastosłupie prawidłowym sześciokątnym 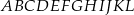 wierzchołki
wierzchołki 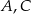 i
i 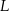 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
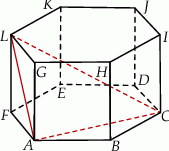
Cosinus największego kąta trójkąta 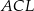 jest równy
jest równy
A)  B)
B) 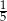 C) 0 D)
C) 0 D) 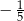
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

