Zadanie nr 9049314
Pięć spośród sześciu różnokolorowych kul wkładamy do pięciu ponumerowanych szuflad tak, że w każdej szufladzie znajduje się jedna kula. Na ile różnych sposobów można to zrobić?
A) 120 B) 720 C) 24 D) 126
Rozwiązanie
Sposób I
Najpierw musimy wybrać pięć kul, które znajdą się w szufladach – można to zrobić na 6 sposobów (wystarczy ustalić, która kula odpada). Potem 5 kul należy umieścić w 5 szufladach – to można zrobić na
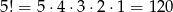
sposobów (pierwszą kulę możemy włożyć na 5 sposobów, drugą na 4, itd.). Łącznie jest więc
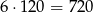
sposobów.
Sposób II
Ustawiamy 6 kul w dowolnej kolejności – możemy to zrobić na
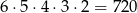
sposobów i pierwsze 5 wkładamy do szuflad. Jest więc 720 takich układów.
Odpowiedź: B

