Zadanie nr 5965020
Zbiorem rozwiązań nierówności 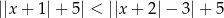 jest
jest
A) 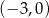 B)
B) 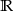 C)
C) 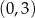 D)
D) 
Rozwiązanie
Daną nierówność możemy zapisać w postaci
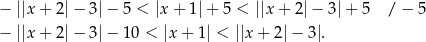
Zauważmy teraz, że lewa nierówność jest zawsze spełniona, więc pozostaje nierówność
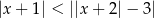
Sposób I
Szkicujemy teraz wykresy funkcji po obu stronach nierówności.
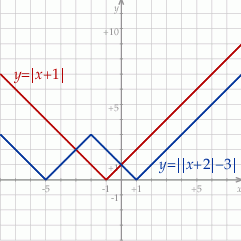
Z wykresu widać, że rozwiązaniem tej nierówności jest przedział 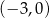 .
.
Sposób II
Podnosimy nierówność stronami do kwadratu
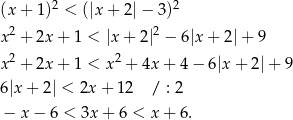
Mamy stąd układ nierówności
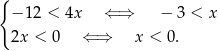
Rozwiązaniem jest więc przedział 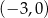 .
.
Odpowiedź: A

