Zadanie nr 7031025
Najmniejsza wartość wyrażenia 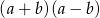 dla
dla 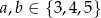 jest równa
jest równa
A) 2 B) 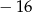 C) 0 D)
C) 0 D) 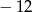
Rozwiązanie
Korzystamy ze wzoru skróconego mnożenia
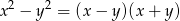
na różnicę kwadratów. Mamy zatem
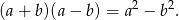
Widać teraz, że najmniejszą wartość tego wyrażenia otrzymamy, gdy 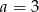 i
i 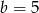 . Wtedy
. Wtedy
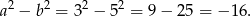
Odpowiedź: B

