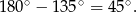Zadanie nr 9816472
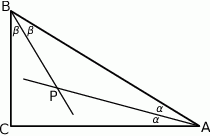
Uzasadnij, że kąt ostry między dwusiecznymi kątów ostrych trójkąta prostokątnego jest równy 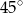 .
.
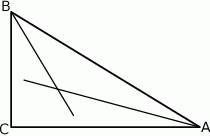
Rozwiązanie
Oznaczmy 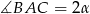 i
i 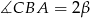 .
.
W takim razie 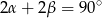 , czyli
, czyli 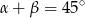 (bo suma kątów w trójkącie
(bo suma kątów w trójkącie 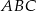 jest równa
jest równa 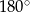 ).
).
Patrzymy teraz na trójkąt 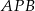 .
.
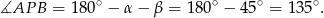
W takim razie kąt ostry między dwusiecznymi ma miarę