Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 3694791

Zdanie „różnica kwadratów dwóch kolejnych liczb naturalnych nieparzystych jest niemniejsza niż 5” przedstawiono w postaci nierówności:
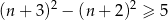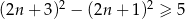
A) (n + 3 )2 − (n + 2 )2 ≥ 5 B) (2n + 3 )2 − (2n + 1)2 ≥ 5
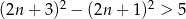C) 2 2 (2n + 3) − (2n + 1 ) > 5 D) 2 [(2n + 3) − (2n + 1 )] ≥ 5

Wersja PDF
Rozwiązanie

Różnica kwadratów dwóch kolejnych nieparzystych liczb naturalnych to

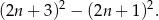
(2n + 3)2 − (2n + 1)2.

Dane zdanie możemy więc zapisać w postaci:

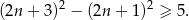
(2n + 3)2 − (2n + 1)2 ≥ 5 .

 
Odpowiedź: B

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!