/Szkoła średnia/Zadania testowe/Liczby/Wyrażenia algebraiczne/Inne/3 literki

Zadanie nr 9418287

Warunek „każda z czterech liczb 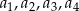a1,a2,a3,a4 jest niezerowa” jest równoważny warunkowi
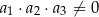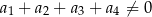
A) a1 ⋅a2 ⋅a 3 ⁄= 0 B) a1 + a2 + a3 + a4 ⁄= 0
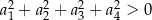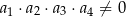
C) 2 2 2 2 a1 + a2 + a3 + a 4 > 0 D) a1 ⋅a2 ⋅ a3 ⋅a4 ⁄= 0

Wersja PDF

Rozwiązanie

Jeżeli liczby 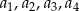a1,a2,a3,a4 są niezerowe to oczywiście

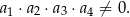
a1 ⋅ a2 ⋅a3 ⋅a4 ⁄= 0.

Odwrotnie też: jeżeli jest spełniony powyższy warunek, żadna z liczb 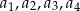a1,a2,a3,a4 nie może być równa 0.  
Odpowiedź: D

Wersja PDF