Zadanie nr 1169617
Dany jest sześcian 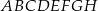 . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 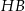 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy 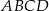 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
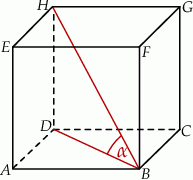
A) 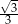 B)
B) 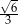 C)
C) 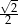 D)
D) 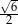
Rozwiązanie
Oznaczmy długość krawędzi sześcianu przez  .
.
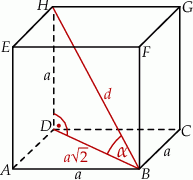
Długość przekątnej sześcianu jest wtedy równa
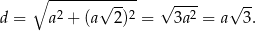
Stąd
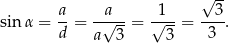
Odpowiedź: A

