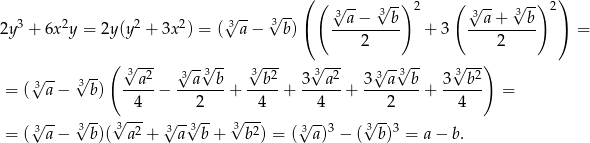Zadanie nr 1623925
Uzasadnij, że jeżeli  i
i 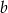 są liczbami całkowitymi i
są liczbami całkowitymi i 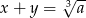 oraz
oraz 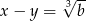 , to
, to 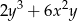 też jest liczbą całkowitą.
też jest liczbą całkowitą.
Rozwiązanie
Sposób I
Wiemy, że 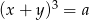 i
i 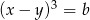 są liczbami całkowitymi, więc różnica tych liczb też jest liczbą całkowitą.
są liczbami całkowitymi, więc różnica tych liczb też jest liczbą całkowitą.
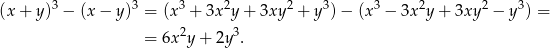
Sposób II
Dodając, a potem odejmując równania układu
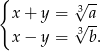
stronami mamy 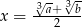 i
i 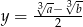 . Stąd
. Stąd